
【题目】如图,在扇形CAB中,CD⊥AB,垂足为D,圆E是△ACD的内切圆,切点分别为M,N,F,连接AE,BE.
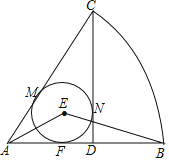
(1)求∠AEB的度数;
(2)若AD=DB,CD=3,求扇形CAB的弧长和圆E的半径.
【答案】(1)∠AEB=135°;(2)扇形CAB的弧长为![]() ,圆E的半径为
,圆E的半径为![]() .
.
【解析】
(1)连接EC.首先求出∠AEC=135°,再证明△EAC≌△EAB即可解决问题;
(2)连接BC、EF、EM、EN、DE,证明△ABC是等边三角形,得出∠BAC=60°,由直角三角形的性质得出AD![]() CD
CD![]() ,得出AB=AC=2
,得出AB=AC=2![]() ,由弧长公式求出扇形CAB的弧长,由切线的性质和三角形面积可求出圆E的半径.
,由弧长公式求出扇形CAB的弧长,由切线的性质和三角形面积可求出圆E的半径.
(1)连接EC.如图1所示:
∵E是△ADC的内心,∠ADC=90°,∴∠ACE![]() ∠ACD,∠EAC
∠ACD,∠EAC![]() ∠CAD,∴∠AEC=180°
∠CAD,∴∠AEC=180°![]() (∠ACD+∠CAD)=135°,
(∠ACD+∠CAD)=135°,
在△AEC和△AEB中,∵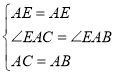 ,∴△EAC≌△EAB(SAS),∴∠AEB=∠AEC=135°;
,∴△EAC≌△EAB(SAS),∴∠AEB=∠AEC=135°;
(2)连接BC、EF、EM、EN、DE,如图2所示:
∵CD⊥AB,AD=DB,∴AC=BC.
∵AC=AB,∴AB=AC=BC,∴△ABC是等边三角形,∴∠BAC=60°,∴∠ACD=30°,∴AD![]() CD
CD![]() ,∴AB=AC=2
,∴AB=AC=2![]() ,∴扇形CAB的弧长为
,∴扇形CAB的弧长为![]() ,
,
∵圆E是△ACD的内切圆,切点分别为M,N,F,∴EF⊥AD,EN⊥CD,EM⊥AC,EM=EF=EN.
∵CD⊥AB,∴△ACD的面积=△ACE的面积+△ADE的面积+△CDE的面积,
即![]() 3
3![]() 2
2![]() EM
EM![]() EF
EF![]() 3×EN,
3×EN,
解得:EF![]() ,
,
即圆E的半径为![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题①相似三角形一定不是全等三角形;②相似三角形对应中线的等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O为△ABC内任意一点,OA、OB、OC的中点分别为![]() 、
、![]() 、
、![]() ,则有△
,则有△![]()
![]()
![]() ∽△ABC.其中正确的个数有( )
∽△ABC.其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价为30元,试销中发现:销售价格为36元/件时,每天销售28件;销售价格为32元/件时,每天销售36件.若这种商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元)存在一次函数,请回答下列问题:
(元)存在一次函数,请回答下列问题:
(1)求出![]() 与
与![]() 的关系式;
的关系式;
(2)设商店销售这种商品每天获利![]() (元),写出
(元),写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
①当商店销售这种商品每天获利150元,销售价格定为多少比较合理;
②销售价格定为多少时,商店获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com