
����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����Ϊ30Ԫ�������з��֣����ۼ۸�Ϊ36Ԫ/��ʱ��ÿ������28�������ۼ۸�Ϊ32Ԫ/��ʱ��ÿ������36��.��������Ʒ��������![]() �����������ۼ۸�
�����������ۼ۸�![]() ��Ԫ������һ�κ�������ش��������⣺
��Ԫ������һ�κ�������ش��������⣺
��1�����![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2�����̵�����������Ʒÿ�����![]() ��Ԫ����д��
��Ԫ����д��![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
�ٵ��̵�����������Ʒÿ�����150Ԫ�����ۼ۸�Ϊ���ٱȽϺ�����
�����ۼ۸�Ϊ����ʱ���̵���������������Ƕ���Ԫ��
���𰸡���1��![]() ����2��
����2��![]() ���ٵ��̵�����������Ʒÿ�����150Ԫ�����ۼ۸�Ӧ��Ϊ35��45Ԫ�������ۼ۸�Ϊ40Ԫʱ���̵����������������200Ԫ.
���ٵ��̵�����������Ʒÿ�����150Ԫ�����ۼ۸�Ӧ��Ϊ35��45Ԫ�������ۼ۸�Ϊ40Ԫʱ���̵����������������200Ԫ.
��������
��1����![]() ��
��![]() �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ![]() ���������ۼ۸�Ϊ36Ԫ/��ʱ��ÿ������28�������ۼ۸�Ϊ32Ԫ/��ʱ��ÿ������36�������ô���ϵ������������ù�ϵʽ��
���������ۼ۸�Ϊ36Ԫ/��ʱ��ÿ������28�������ۼ۸�Ϊ32Ԫ/��ʱ��ÿ������36�������ô���ϵ������������ù�ϵʽ��
��2�����ݡ��������۵��ۣ����ۣ��������������ɵó�![]() ����
����![]() �ĺ�����ϵʽ������
�ĺ�����ϵʽ������![]() �����
�����![]() ֵ�����ɵó����ۣ��������䷽���ó�
ֵ�����ɵó����ۣ��������䷽���ó�![]() �����ö��κ��������ʼ��ɽ����ֵ����.
�����ö��κ��������ʼ��ɽ����ֵ����.
�⣺��1����![]() ��
��![]() �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ![]() ��
��
��������ã�![]() ����ã�
����ã�![]() ��
��
��![]() ��
��![]() �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ![]() .
.
��2������֪�ã�![]() .
.
����![]() ����
����![]() ��
��
��ã�![]() ��
��![]() .
.
�𣺵��̵�����������Ʒÿ�����150Ԫ�����ۼ۸�Ӧ��Ϊ35��45Ԫ.
�ڡ�![]() ��
��
�൱![]() ʱ��
ʱ��![]() ȡ���ֵ�����ֵΪ200.
ȡ���ֵ�����ֵΪ200.
�����ۼ۸�Ϊ40Ԫʱ���̵����������������200Ԫ.


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��A��4��0����B��1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��

��1���������ߵı���ʽ��
��2��ֱ��д����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ�ڵ������ޣ�����ABP�����Ϊ6ʱ�������P�����ꣻ
��4������M��ֱ��BH���˶�����N��x�����˶�����CM=MN������CMN=90��ʱ�����ʱ��CMN�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ����
��ͼ����![]() ���㣬����
���㣬����![]() ��
��![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ����
����![]() ��
��
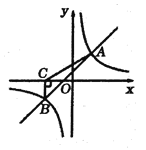
��1����һ�κ����뷴���������ı���ʽ��
��2������������������ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
��3����![]() �Ƿ���������
�Ƿ���������![]() ͼ���ϵ����㣬��
ͼ���ϵ����㣬��![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����I����ABC�����ģ���AIC=124������E��AD���ӳ����ϣ����CDE�Ķ���Ϊ��������

A. 56�� B. 62�� C. 68�� D. 78��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������CAB�У�CD��AB������ΪD��ԲE����ACD������Բ���е�ֱ�ΪM��N��F������AE��BE.
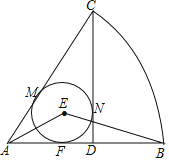
��1�����AEB�Ķ�����
��2����AD��DB��CD��3��������CAB�Ļ�����ԲE�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA��3��OC��2��F��AB�ϵ�һ������(F����A��B�غ�)������F�ķ���������y��![]() (x��0)��ͼ����BC�߽��ڵ�E.
(x��0)��ͼ����BC�߽��ڵ�E.
(1)��FΪAB���е�ʱ����ú����Ľ���ʽ��
(2)��kΪ��ֵʱ����EFA���������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
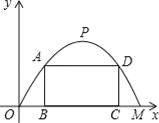
����Ŀ��ʩ����Ҫ��һ�������Ϊ�����ߵĹ�·��������߶�Ϊ6�ף�����OMΪ12�ף�����O��Ϊԭ�㣬OM����ֱ��Ϊx�Ὠ��ֱ������ϵ����ͼ��ʾ����
��1��ֱ��д����M�������߶���P�����ꣻ
��2��������������ߵĺ�������ʽ��
��3��ʩ���Ӽƻ��������ſڴһ�����������ּ���ABCD��ʹA��D�����������ϣ�B��C���ڵ���OM�ϣ�Ϊ�˳ﱸ���ϣ�����������ּ�������ľ��AB��AD��DC�ij���֮�͵����ֵ�Ƕ��٣������ʩ���Ӽ���һ�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ۽Ǧ��������������Ǻ���ֵ���£�
sin��=sin��180�㩁������cos��=��cos��180�㩁����
��1����sin120�㣬cos120�㣬sin150���ֵ��
��2����һ�������ε������ڽǵı���1��1��4��A��B����������ε��������㣬sinA��cosB�Ƿ���4x2��mx��1=0����������ȵ�ʵ��������m��ֵ����A����B�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c�У�����y���Ա���x�IJ��ֶ�Ӧֵ�����
x | �� | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | m | 5 | 2 | 1 | 2 | �� |
��m��ֵ��_____����y��5ʱ��x��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com