
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,且
,且![]() 。
。
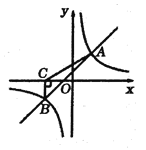
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() 的解集;
的解集;
(3)若![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)把![]() 的坐标代入一次函数的解析式,得到
的坐标代入一次函数的解析式,得到![]() ,再根据以
,再根据以![]() 为底的三角形ABC的面积为5求得m和n的值,继而求得一次函数与反比例函数的表达式;
为底的三角形ABC的面积为5求得m和n的值,继而求得一次函数与反比例函数的表达式;
(2)根据![]() 的横坐标,结合图象即可得出答案;
的横坐标,结合图象即可得出答案;
(3)分为两种情况:当点P在第三象限和在第一象限上时,根据坐标和图象即可得出答案.
解:
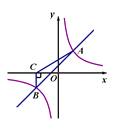
(1)∵点![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
而![]() ,且
,且![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (舍去),则
(舍去),则![]() ,
,
由![]() ,得
,得![]() ,
,
∴一次函数的表达式为![]() ;
;
又将![]() 代入
代入![]() ,得
,得![]() ,
,
∴反比例函数的表达式为![]() ;
;
(2)不等式![]() 的解集为
的解集为![]() 或
或![]() ;
;
(3)∵点![]() 在反比例函数
在反比例函数![]() 图象上,且点
图象上,且点![]() 在第三象限内,
在第三象限内,
∴当点![]() 在第一象限内时,总有
在第一象限内时,总有![]() ,此时,
,此时,![]() ;
;
当点![]() 在第三象限内时,要使
在第三象限内时,要使![]() ,
,![]() ,
,
∴满足![]() 的
的![]() 的取值范围是
的取值范围是![]() 或
或![]() 。
。


科目:初中数学 来源: 题型:
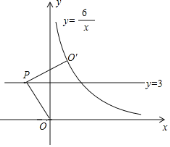
【题目】如图,点P是直线y=3上的动点,连接PO并将PO绕P点旋转90°到PO′,当点O′刚好落在双曲线![]() (x>0)上时,点P的横坐标所有可能值为_____.
(x>0)上时,点P的横坐标所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,反比例函数y=![]() (m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
(m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
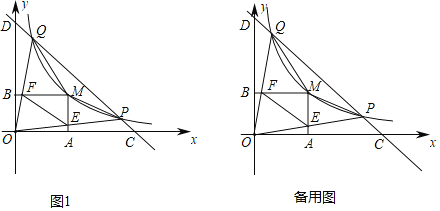
(1)当m=4时,求线段CD的长;
(2)当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,求此时点M的坐标;
(3)当2<x<m时,记以线段OE,OF为两直角边的三角形外接圆面积为S1;记三角形△MEF的外接圆面积为S2;记以PC为直径的圆面积为S3;记以QD为直径的圆面积为S4;试比较S1,S2+S3+S4的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
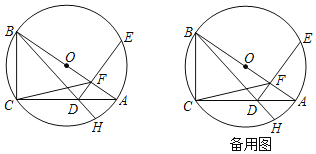
【题目】如图,![]() 是
是![]() 的内接三角形,AB为
的内接三角形,AB为![]() 直径,
直径,![]() ,
,![]() ,点D为线段AC上一动点,过点D作AB的垂线交
,点D为线段AC上一动点,过点D作AB的垂线交![]() 于点E,交AB于点F,连结BD,CF,并延长BD交
于点E,交AB于点F,连结BD,CF,并延长BD交![]() 于点H.
于点H.
![]() 求
求![]() 的半径;
的半径;
![]() 当DE经过圆心O时,求AD的长;
当DE经过圆心O时,求AD的长;
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题①相似三角形一定不是全等三角形;②相似三角形对应中线的等于对应角平分线的比;③边数相同,对应角相等的两个多边形相似;④O为△ABC内任意一点,OA、OB、OC的中点分别为![]() 、
、![]() 、
、![]() ,则有△
,则有△![]()
![]()
![]() ∽△ABC.其中正确的个数有( )
∽△ABC.其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价为30元,试销中发现:销售价格为36元/件时,每天销售28件;销售价格为32元/件时,每天销售36件.若这种商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元)存在一次函数,请回答下列问题:
(元)存在一次函数,请回答下列问题:
(1)求出![]() 与
与![]() 的关系式;
的关系式;
(2)设商店销售这种商品每天获利![]() (元),写出
(元),写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
①当商店销售这种商品每天获利150元,销售价格定为多少比较合理;
②销售价格定为多少时,商店获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
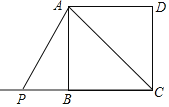
【题目】如图,在正方形ABCD中,点P在线段CB的延长线上,连接PA,将线段PA绕点P顺时针旋转90°,得到线段PE,连接CE,过点E作EF⊥BC于H,与对角线AC交于点F.
(1)请根据题意补全图形;
(2)求证:EH=FH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com