
【题目】如图1,在平面直角坐标系中,反比例函数y=![]() (m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
(m为常数,m>2,x>0)的图象过点P(m,2)和Q(2,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是反比例函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.MA交OP于点E,MB交OQ于点F,连接EF,MP,MQ
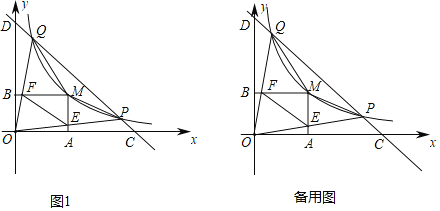
(1)当m=4时,求线段CD的长;
(2)当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,求此时点M的坐标;
(3)当2<x<m时,记以线段OE,OF为两直角边的三角形外接圆面积为S1;记三角形△MEF的外接圆面积为S2;记以PC为直径的圆面积为S3;记以QD为直径的圆面积为S4;试比较S1,S2+S3+S4的大小.
【答案】(1) 6![]() ;(2) M(4,4);(3) S1=S2+S3+S4,理由见解析
;(2) M(4,4);(3) S1=S2+S3+S4,理由见解析
【解析】
(1)求出直线PQ的解析式,再求出点C,D的坐标即可解决问题.
(2)由题意当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,根据反比例函数是关于直线y=x对称的,可知点M在直线y=x上,可得M(![]() ,
,![]() ),然后求出直线PQ的解析式,连接OM交CD于G,求出OG,OM,可得MG的长,然后结合P,Q坐标,可得PQ的长,再利用三角形的面积公式构建方程即可解决问题;
),然后求出直线PQ的解析式,连接OM交CD于G,求出OG,OM,可得MG的长,然后结合P,Q坐标,可得PQ的长,再利用三角形的面积公式构建方程即可解决问题;
(3)设M(a,![]() ),由(2)可知D(0,2+m),C(2+m,0),可得DQ=
),由(2)可知D(0,2+m),C(2+m,0),可得DQ=![]() ,PC=
,PC=![]() ,然后易得直线OP的解析式为y=
,然后易得直线OP的解析式为y=![]() ,直线OQ的解析式为y=
,直线OQ的解析式为y=![]() ,求出E(a,
,求出E(a,![]() ),F(
),F(![]() ,
,![]() ),再根据直角三角形外接圆的性质和圆的周长公式求出S1,S2,S3,S4,即可判断.
),再根据直角三角形外接圆的性质和圆的周长公式求出S1,S2,S3,S4,即可判断.
解:(1)当m=4时,Q(2,4),P(4,2),
设直线PQ的解析式为y=kx+b(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线PQ的解析式为y=﹣x+6,
令y=0则x=6,令x=0则y=6,
∴C(6,0),D(0,6),
∴OC=OD=6,
∵∠COD=90°,
∴CD=![]() ;
;
(2)∵当2<x<m时,若仅存在唯一的点M使得△MPQ的面积等于m﹣2,
∴根据反比例函数关于直线y=x对称,可知点M在直线y=x上,
∴M(![]() ,
,![]() ),
),
∴OM=![]() ,
,
设直线PQ的解析式为y=kx+b(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线PQ的解析式为y=﹣x+2+m,
令x=0则y=2+m,令y=0则x=2+m,
∴D(0,2+m),C(2+m,0),
∴CD=![]() ,
,
连接OM交CD于G,
∵△COD是等腰直角三角形,点M在直线y=x上,
∴OG⊥CD,
∴OG=![]() ,
,
∴MG=![]() ,
,
∵P(m,2),Q(2,m),
∴PQ=![]() ,
,
由题意得: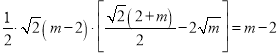 ,
,
解得m=8或0(舍去),
∴M(4,4);
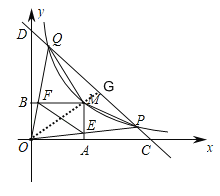
(3)设M(a,![]() ),
),
由(2)可得D(0,2+m),C(2+m,0)
∴DQ=![]() ,PC=
,PC=![]() ,
,
易得直线OP的解析式为y=![]() ,直线OQ的解析式为y=
,直线OQ的解析式为y=![]() ,
,
∴E(a,![]() ),F(
),F(![]() ,
,![]() ),
),
∴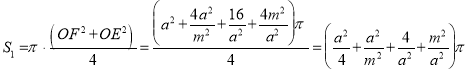
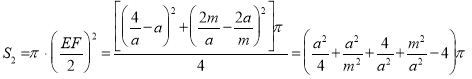 ,
,
S3=S4=2π,
∴S2+S3+S4=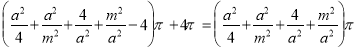 =S1,
=S1,
∴S1=S2+S3+S4.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD,△BCE,△ABC的面积分别是S1,S2,S3,现有如下结论:
①S1∶S2=AC2∶BC2;②连接AE,BD,则△BCD≌△ECA;③若AC⊥BC,则S1·S2=![]() S23.
S23.
其中结论正确的序号是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.

(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当CM=MN,且∠CMN=90°时,求此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
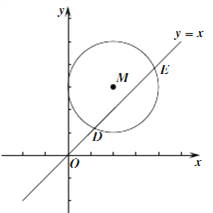
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,且
,且![]() 。
。
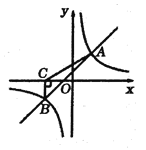
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() 的解集;
的解集;
(3)若![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
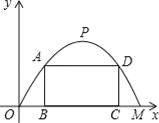
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com