
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() .
.
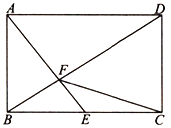
(1)若![]() ,求
,求![]() 的长;
的长;
(2)在(1)的条件下,连接![]() ,求
,求![]() 的长.
的长.
【答案】(1)2;(2)![]()
【解析】
(1)根据四边形ABCD是矩形,得到∠ABE=∠BAD=90°,根据余角的性质得到∠BAE=∠ADB,根据相似三角形的性质得到BE=1,求得BC=2,
(2)根据勾股定理得到AE=![]() =
=![]() ,BD=
,BD=![]() ,根据三角形的面积公式得到BF=
,根据三角形的面积公式得到BF=![]() ,过F作FG⊥BC于G,根据相似三角形的性质得到CG=
,过F作FG⊥BC于G,根据相似三角形的性质得到CG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
解:(1)∵四边形ABCD是矩形,
∴∠ABE=∠BAD=90°,
∵AE⊥BD,
∴∠AFB=90°,
∴∠BAE+∠ABD=∠ABD+∠ADB=90°,
∴∠BAE=∠ADB,
∴△ABE∽△DAB,
∴![]() ,
,
∵E是BC的中点,
∴AD=2BE,
∴2BE2=AB2=2,
∴BE=1,
∴BC=2.
(2)∵BC=2,点![]() 是
是![]() 的中点,
的中点,
∴AE=![]() =
=![]() ,BD=
,BD=![]() ,
,
∴由面积相等法可得BF=![]() ,
,
过F作FG⊥BC于G,如图,
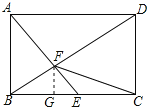
∴FG∥CD,
∴△BFG∽△BDC,
∴![]() ,
,
∴FG=![]() ,BG=
,BG=![]() ,
,
∴CG=![]() ,
,
∴CF=![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在扇形CAB中,CD⊥AB,垂足为D,圆E是△ACD的内切圆,切点分别为M,N,F,连接AE,BE.
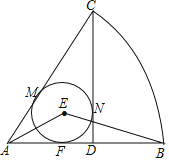
(1)求∠AEB的度数;
(2)若AD=DB,CD=3,求扇形CAB的弧长和圆E的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过点A(3﹣m,4),且过点B(3+m,4),A在B的左侧,顶点为P.
(1)求b的值;
(2)当c=4时,求sin∠APB;
(3)抛物线y=x2+bx+c上是否存在点Q,使得四边形OPQA是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵![]() ≥0,
≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b=2
,(只有当a=b时,a+b=2![]() ).
).
即当a=b时,a+b取得最小值,且最小值为2![]() .
.
根据上述内容,回答下列问题:
问题1:若m>0,当m= 时,m+![]() 有最小值为 ;
有最小值为 ;
问题2:若函数y=a+![]() ,则当a= 时,函数y=a+
,则当a= 时,函数y=a+![]() 有最小值为 ;
有最小值为 ;
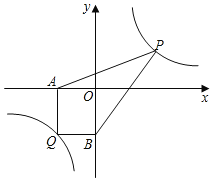
(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() 上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为
,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为![]() ,则其升高可能是( )
,则其升高可能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | m | 5 | 2 | 1 | 2 | … |
则m的值是_____,当y<5时,x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
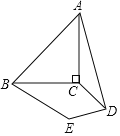
【题目】如图,等腰直角三角形ABC的斜边AB=![]() ,将线段AB绕着点A逆时针旋转60°,点B的对应点为D,连接CD,将线段CD绕点D逆时针旋转60°,点C的对应点为E,连接BE,则∠ABE=_____°.
,将线段AB绕着点A逆时针旋转60°,点B的对应点为D,连接CD,将线段CD绕点D逆时针旋转60°,点C的对应点为E,连接BE,则∠ABE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
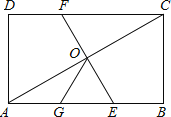
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,若点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)△OGE是等边三角形;(2)DC=3OG;(3)OG=![]() BC;(4)S△AOE=
BC;(4)S△AOE=![]() S矩形ABCD
S矩形ABCD
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,体育老师随机抽取了九年级甲、乙两班部分女生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和频数直方图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)将频数直方图补充完整;
(3)如果该校九年级共有女生360人,估计仰卧起坐能够一分钟完成30次或30次以上的女学生有多少人?
(4)已知第一组有两名甲班学生,第四组中只有一名乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com