
【题目】已知抛物线y=x2+bx+c经过点A(3﹣m,4),且过点B(3+m,4),A在B的左侧,顶点为P.
(1)求b的值;
(2)当c=4时,求sin∠APB;
(3)抛物线y=x2+bx+c上是否存在点Q,使得四边形OPQA是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)b=﹣6;(2)![]() ;(3)存在点Q的坐标分别是(5,7)或(1,﹣17),使得四边形OPQA是平行四边形
;(3)存在点Q的坐标分别是(5,7)或(1,﹣17),使得四边形OPQA是平行四边形
【解析】
(1)求出抛物线的对称轴方程为x=3,则b的值可求出;
(2)过点B作BM⊥AP于点M,求出点P,A,B的坐标,求出AP长,根据三角形PAB的面积可求出BM长,则可求出sin∠APB;
(3)由题意得出点A的坐标为(3﹣m,4),点P的坐标为(3,4﹣m2),由平行四边形的性质可得点Q的坐标为Q(3+3﹣m,4﹣m2+4),代入抛物线解析式可求出m的值,则点Q的坐标可求出.
解:(1)由抛物线的对称性可知,对称轴是直线x=![]() ,
,
又∵对称轴是直线x=﹣![]() ,
,
∴b=﹣6;
(2)当c=4时,由(1)得到抛物线的表达式为y=x2﹣6x+4=(x﹣3)2﹣5,
∴点P的坐标为(3,﹣5).
由x2﹣6x+4=4得x1=0,x2=6,
∴点A,B的坐标分别为(0,4),(6,4),
如图,AB与抛物线的对称轴交于点N,过点B作BM⊥AP于点M,
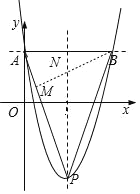
∴PN=5+4=9,AB=6,![]() =3
=3![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴sin∠APB=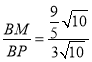 =
=![]() ;
;
(3)存在点Q,使得四边形OPQA是平行四边形.理由是:
由(1)得抛物线为y=x2﹣6x+c,点A的坐标为(3﹣m,4),
求得c=13﹣m2,
∴点P的坐标为(3,4﹣m2),
∴抛物线的表达式为y=x2﹣6x+c=x2﹣6x+13﹣m2,
将线段OA平移,使点O与点P重合,得到线段PQ,
此时四边形OPQA是平行四边形.
由平移的性质可得,点Q的坐标为Q(3+3﹣m,4﹣m2+4),
即Q(6﹣m,8﹣m2),
若点Q在抛物线上,
有8﹣m2=(6﹣m)2﹣6(6﹣m)+13﹣m2.
解得m1=1,m2=5,
当m1=1时,点Q(5,7),
当m2=5时,点Q(1,﹣17).
综合以上可得,存在点Q的坐标分别是(5,7)或(1,﹣17),使得四边形OPQA是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)

查看答案和解析>>
科目:初中数学 来源: 题型:
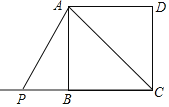
【题目】如图,在正方形ABCD中,点P在线段CB的延长线上,连接PA,将线段PA绕点P顺时针旋转90°,得到线段PE,连接CE,过点E作EF⊥BC于H,与对角线AC交于点F.
(1)请根据题意补全图形;
(2)求证:EH=FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
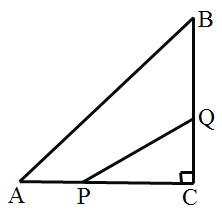
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 沿
沿![]() 向
向![]() 以
以![]() 的速度移动,到
的速度移动,到![]() 即停,点
即停,点![]() 从点
从点![]() 沿
沿![]() 向
向![]() 以
以![]() 的速度移动,到
的速度移动,到![]() 就停.
就停.
(1)若![]() 同时出发,经过几秒钟
同时出发,经过几秒钟![]() ;
;
(2)若点![]() 从
从![]() 点出发
点出发![]() 后点
后点![]() 从点
从点![]() 出发,再经过几秒
出发,再经过几秒![]() 与
与![]() 相似.
相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com