
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=![]() AC
AC
(1)求过点A,B的直线的函数表达式;
(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.

【答案】(1)y=![]() x+
x+![]() ;(2)D点位置见解析,D(
;(2)D点位置见解析,D(![]() ,0);(3)符合要求的m的值为
,0);(3)符合要求的m的值为![]() 或
或![]() .
.
【解析】
(1)先根据A(3,1),C(1,0),求出AC进而得出BC=3求出B点坐标,利用待定系数法求出直线AB的解析式即可;
(2)运用相似三角形的性质就可求出点D的坐标;
(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题.
解:(1)∵A(﹣3,0),C(1,0),
∴AC=4,
∵BC=![]() AC,
AC,
∴BC=![]() ×4=3,
×4=3,
∴B(1,3),
设直线AB的解析式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为y=![]() x+
x+![]() ;
;
(2)若△ADB与△ABC相似,过点B作BD⊥AB交x轴于D,
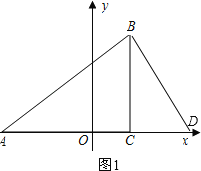
∴∠ABD=∠ACB=90°,如图1,
此时![]() =
=![]() ,即AB2=ACAD.
,即AB2=ACAD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=![]() ,
,
∴OD=AD﹣AO=![]() ﹣3=
﹣3=![]() ,
,
∴点D的坐标为(![]() ,0);
,0);
(3)∵AP=DQ=m,
∴AQ=AD﹣QD=![]() ﹣m.
﹣m.
Ⅰ、若△APQ∽△ABD,如图2,

则有![]() =
=![]() ,
,
∴APAD=ABAQ,
∴![]() m=5(
m=5(![]() ﹣m),
﹣m),
解得m=![]() ;
;
Ⅱ、若△APQ∽△ADB,如图3,
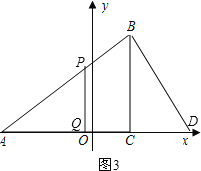
则有![]() =
=![]() ,
,
∴APAB=ADAQ,
∴5m=![]() (
(![]() ﹣m),
﹣m),
解得:m=![]() ,
,
综上所述:符合要求的m的值为![]() 或
或![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:
sinα=sin(180°﹣α),cosα=﹣cos(180°﹣α)
(1)求sin120°,cos120°,sin150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2﹣mx﹣1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | m | 5 | 2 | 1 | 2 | … |
则m的值是_____,当y<5时,x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,若点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)△OGE是等边三角形;(2)DC=3OG;(3)OG=![]() BC;(4)S△AOE=
BC;(4)S△AOE=![]() S矩形ABCD
S矩形ABCD
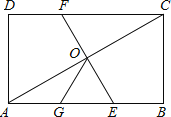
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
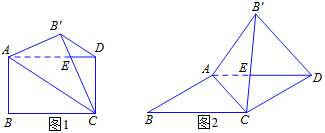
【题目】折纸是一项有趣的活动,在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念. 今天,就让我们带着数学的眼光来玩一玩折纸.
实践操作
如图1,将矩形纸片ABCD沿对角线AC翻折,使点![]() 落在矩形ABCD所在平面内,
落在矩形ABCD所在平面内,![]() C和AD相交于点E,连接
C和AD相交于点E,连接![]() D.
D.
解决问题
(1)在图1中,①![]() D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
D和AC的位置关系是_____;②将△AEC剪下后展开,得到的图形是____;
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
拓展应用
(3)在图2中,若∠B=30o,AB=![]() ,当A
,当A![]() ⊥AD时,BC的长度为_____.
⊥AD时,BC的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k+1)x+k2﹣2=0
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两个实数根为x1、x2,且满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com