
【题目】在平面直角坐标系xOy中,直线l:y=kx+b(k≠0)与直线y=kx(k≠0)平行,与直线y=3相交于点A(3,3).
(1)求k和b的关系式;
(2)横、纵坐标都是整数的点叫做整点,记直线l:y=kx+b、y=kx、y=3与x轴构成的封闭区域(不含边界)为W.
①当k=2时,结合函数图象,求区域W内的整点个数;
②若区域W内恰有2个整点,直接写出k的取值范围.
【答案】(1)b=3﹣3k;(2)①W区域内有2个整数点(1,1),(2,2),②1<k≤2
【解析】
(1)根据题意列方程即可得到结论;
(2)①当k=2时,得到b=3﹣3k=﹣3,求得直线l:y=2x﹣3(k≠0)与直线y=2x与x轴的交点为(![]() ,0),(0,0),与直线y=3的交点为(3,3),(
,0),(0,0),与直线y=3的交点为(3,3),(![]() ,3)于是得到结论;
,3)于是得到结论;
②当直线y=kx(k≠0)经过(2,2)时,此时求得直线的解析式为y=x,得到直线l的解析式也为y=x,此时区域W内没有整点,由①知,当区域W内恰有2个整点时,k=2,于是得到结论.
解:(1)直线l:y=kx+b(k≠0)与直线y=3相交于点A(3,3),
∴3k+b=3,
∴b=3﹣3k;
(2)①当k=2时,则b=3﹣3k=﹣3,
∴直线l:y=2x﹣3(k≠0)与直线y=2x平行,分别与x轴的交点为(![]() ,0),(0,0),
,0),(0,0),
分别与直线y=3的交点为(3,3),(![]() ,3),
,3),
在W区域内有2个整数点:(1,1),(2,2);
②当直线y=kx(k≠0)经过(2,2)时,此时,直线的解析式为y=x,
∵直线l:y=kx+b(k≠0)与直线y=kx(k≠0)平行且经过点A(3,3).
∴直线l的解析式也为y=x,
此时区域W内没有整点,
由①知,当区域W内恰有2个整点时,k=2,
综上所述,若区域W内恰有2个整点,k的取值范围为:1<k≤2.


科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
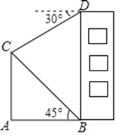
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
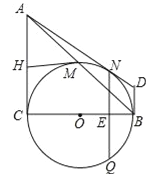
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
(1)求证:MH为⊙O的切线.
(2)若MH=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
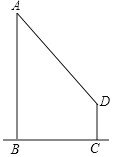
【题目】如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
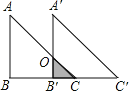
【题目】如图所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,现将△ABC沿BC方向平移到△A′B′C′的位置.若平移的距离为3,则△ABC与△A′B′C′重叠部分的阴影面积为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=![]() BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
BE;②∠A=∠BHE;③AB=BH;④△BHD∽△BDG.其中正确的结论是( )
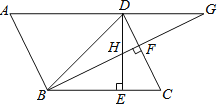
A.①②③④B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
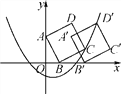
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
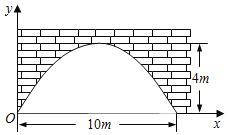
【题目】有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)一辆宽为2米,高为3米的货船能否从桥下通过?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com