
分析 首先解不等式组求得x的范围,根据不等式组有4个整数解即可得到关于m的不等式,从而求解.
解答 解:$\left\{\begin{array}{l}{\frac{x+3}{2}≥4}\\{x<m}\end{array}\right.$,
解$\frac{x+3}{2}≥4$得:x≥5,
则不等式组的解集是:5≤x<m.
∵等式组$\left\{\begin{array}{l}{\frac{x+3}{2}≥4}\\{x<m}\end{array}\right.$有4个整数解,
∴8<m≤9.
故答案是:8<m≤9.
点评 本题考查了一元一次不等式组的整数解:解决此类问题的关键在于正确解得不等式组,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件求得不等式组的整数解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
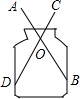 如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
如图,小明家有一个玻璃容器,他想测量一下它的内径是多少?但是他无法将刻度尺伸进去直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com