
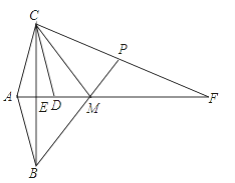
【题目】已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
【答案】见解析
【解析】(1)利用中心对称图形的性质以及轴对称图形的性质得出全等三角形进而得出对应线段相等;
(2)利用(1)中所求,进而得出对应角相等,进而得出答案.
解:(1)证明:∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM,
∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,
∴AB=CD,
∴AC=CD;
(2)∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM∠PMF=αβ,
∠MCD=∠CDE∠DMC=αβ,
∴∠F=∠MCD.


科目:初中数学 来源: 题型:
【题目】某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其 他两位成员交流的情况.
小张:“该商品的进价为 24元/件.”
成员甲:“当定价为 40元/件时,每天可售出 480件.”
成员乙:“若单价每涨 1元,则每天少售出 20件;若单价每降 1元,则每天多售出 40件.” 根据他们的对话,请你求出要使该商品每天获利 7680元,应该怎样合理定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
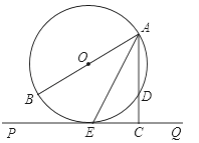
【题目】如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=2,EC=![]() ,∠BAC=60°,求⊙O的半径.
,∠BAC=60°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月12日是母亲节,小明去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支5元,兰花每支3元,小明只有30元,希望购买花的支数不少于7支,其中至少有一支是康乃馨.
(1)小明一共有多少种可能的购买方案?列出所有方案;
(2)如果小明先购买一张2元的祝福卡,再从(1)中任选一种方案购花,求他能实现购买愿望的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
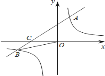
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一、三象限内的
的图象交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
(1)求该反比例函数和一次函数的解析式,并写出使![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(2)若![]() 是直线
是直线![]() 上一点,使得
上一点,使得![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
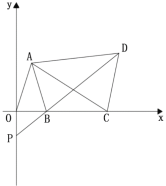
【题目】如图,平面直角坐标系中,已知点![]() 且
且![]() 为
为![]() 轴上点
轴上点![]() 右侧的动点,以
右侧的动点,以![]() 为腰作等腰
为腰作等腰![]() ,使
,使![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点![]() 运动时,点
运动时,点![]() 在
在![]() 轴上的位置是否发生改变,为什么?
轴上的位置是否发生改变,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com