
分析 (1)把两组数据代入二次函数解析式,然后利用待定系数法求解即可;
(2)设购进A产品m吨,购进B产品(10-m)吨,销售A、B两种产品获得的利润之和为W元,根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式,再根据二次函数的最值问题解答.
解答 解:(1)将x=1,y=7;x=2,y=12代入y=ax2+bx得:
$\left\{\begin{array}{l}{a+b=7}\\{4a+2b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=8}\end{array}\right.$.
答:a=-1,b=8;
(2)设购进A产品m吨,购进B产品(10-m)吨,销售A、B两种产品获得的利润之和为W元,
则W=-m2+8m+2(10-m)=-m2+6m+20=-(m-3)2+29,
∵-1<0,
∴当m=3时,W有最大值29万,
∴购进A产品3吨,购进B产品7吨,销售A、B两种产品获得的利润之和最大,最大利润是29万元.
点评 本题考查了二次函数的应用,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,比较简单,(2)整理得到所获利润与购进A产品的吨数的关系式是解题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
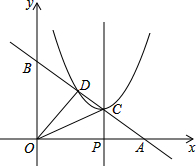 已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.
已知直线y=-$\frac{3}{4}x+3$分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒,以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D,设△COD的OC边上的高为h,当t=$\frac{36}{25}$时,h的值最大.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
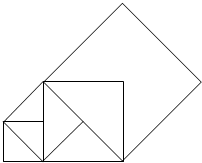 如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.
如图,先画一个边长为1的正方形,以其对角线为边画第二个正方形,再以第二个正方形的对角线为边画第三个正方形,…,如此反复下去,那么第n个正方形的对角线长为($\sqrt{2}$)n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.
如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com