
 如图,在半径为2的⊙O中,弦AB长为2.
如图,在半径为2的⊙O中,弦AB长为2.分析 (1)过点O作OC⊥AB于点C,证出△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离;
(2)证出△ABO是等边三角形得出∠AOB=60°. 再分两种情况:点C在优弧$\widehat{ACB}$上,则∠BCA=30°;点C在劣弧$\widehat{AB}$上,则∠BCA=$\frac{1}{2}$(360°-∠AOB)=150°;即可得出结果.
解答 解: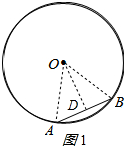 (1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
(1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
∵OD⊥AB且过圆心,AB=2,
∴AD=$\frac{1}{2}$AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD=$\sqrt{A{O}^{2}-A{D}^{2}}$=$\sqrt{3}$.
即点O到AB的距离为$\sqrt{3}$.
(2)如图2所示:
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,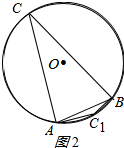
∴∠AOB=60°.
若点C在优弧$\widehat{ACB}$上,则∠BCA=30°;
若点C在劣弧$\widehat{AB}$上,则∠BCA=$\frac{1}{2}$(360°-∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
点评 此题考查了垂径定理、等边三角形的判定与性质、三角函数、弧长公式.熟练掌握垂径定理,证明△OAB是等边三角形是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
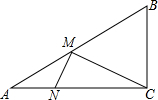 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动.
如图,在△ABC中,∠ACB=90°,AC=8,BC=6,动点M从A点出发,以每秒2个单位长度的速度向B点运动;动点N也从A点同时出发,以每秒1个单位长度的速度向C点运动.当M,N有一点到达终点时,两点都停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -0.01<x<0.02 | B. | 6.17<x<6.18 | C. | 6.18<x<6.19 | D. | 6.19<x<6.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com