
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC,其中正确结论的序号是______.
EC,其中正确结论的序号是______.

【答案】①②④⑤.
【解析】
过P作PG⊥AB于点G,根据正方形对角线的性质及题中的已知条件,证明△AGP≌△FPE后即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=![]() EC.
EC.
证明:过P作PG⊥AB于点G,
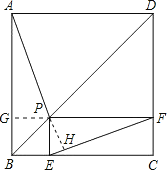
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,
∴∠GPB=45°,
∴GB=GP,
同理,得PE=BE,
∵AB=BC=GF,
∴AG=AB-GB,FP=GF-GP=AB-GB,
∴AG=PF,
∴△AGP≌△FPE,
∴AP=EF,故①正确;
延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,即AP⊥EF,故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∴∠PFE=∠BAP,故④正确;
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=DF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=![]() EC,故⑤正确.
EC,故⑤正确.
∴其中正确结论的序号是①②④⑤.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,点M为直线AB,CD所确定的平面内的一点,若∠A105,∠M108,请直接写出∠C的度数 ;
(2)如图2,AB∥CD,点P为直线AB,CD所确定的平面内的一点,点E在直线CD上,AN平分∠PAB,射线AN的反向延长线交∠PCE的平分线于M,若∠P30,求∠AMC的度数;
(3)如图3,点P与直线AB,CD在同一平面内,AN平分∠PAB,射线AN的反向延长线交∠PCD的平分线于M,若AMC180![]() P,求证:AB∥CD.
P,求证:AB∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计),第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车,小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林,离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
(1)求第一班车从入口处到达塔林的时间.
(2)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变).
(3)若小聪在8:30至8:50之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过3分钟的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
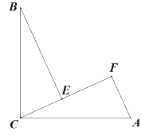
【题目】如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0<∠ACF<45°.
(1)求证:△BEC≌△CEA;
(2)若AF=5,EF=8,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为A的抛物线y=a(x+2)2﹣4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式;
(2)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,OB=AP;
(3)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
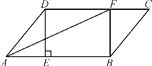
【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com