
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.

【答案】(1)![]() ;(2)
;(2)![]() ; (3) 当
; (3) 当![]() 为
为![]() 时,
时,![]() .
.
【解析】
(1)由于线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,根据旋转的性质得AB=AC,∠BAC=α,利用等腰三角形的性质和三角形内角和定理得到![]() 再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD进行计算;
再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD进行计算;
(2)由线段AB绕点B顺时针旋转60°得线段BE,根据旋转的性质得AB=AE,∠BAE=60°,则AC=AE,∠CAE=60°-α,利用等腰三角形的性质和三角形内角和得到![]() 然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
(3)由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得BC=BD,∠CBD=60°,则可判断△BCD为等腰直角三角形,则∠BCD=60°,CD=BC,
所以∠DCE=∠BCE-∠BCD=90°,加上∠DEC=45°,于是△DEC为等腰直角三角形,则CE=CD,所以CB=CE,然后利用“SSS”证明△ABC≌△AEC,得到∠BAC=∠EAC,所以![]()
![]() ∵线段
∵线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,
∴![]() ;
;

![]() ∵线段
∵线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;![]() 如图②,
如图②,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
当![]() 为
为![]() 时,
时,![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )

A.2B.0.5C.13D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() 的函数表达式为
的函数表达式为![]() ,且直线
,且直线![]() 与x轴交于点D.直线
与x轴交于点D.直线![]() 与x轴交于点A,且经过点B(4,1),直线
与x轴交于点A,且经过点B(4,1),直线![]() 与
与![]() 交于点
交于点![]() .
.

(1)求点D和点C的坐标;
(2)求直线![]() 的函数表达式;
的函数表达式;
(3)利用函数图象写出关于x,y的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
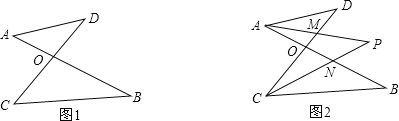
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,当∠D=40°,∠B=30°度时,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com