
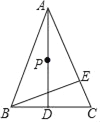
【题目】如图,△ABC中,AB=AC=13,BC=10,AD⊥BC,BE⊥AC,P为AD上一动点,则PE+PC的最小值为__________.
【答案】![]()
【解析】
根据题意作E关于AD的对称点M,连接CM交AD于P,连接EF,过C作CN⊥AB于N,根据三线合一定理求出BD的长和AD⊥BC,根据勾股定理求出AD,根据三角形面积公式求出CN,根据对称性质求出CP+EP=CM,根据垂线段最短得出CP+EP≥![]() ,即可得出答案.
,即可得出答案.
作E关于AD的对称点M,连接CM交AD于P,连接EP,过C作CN⊥AB于N,
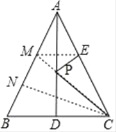
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,由勾股定理得:AD=![]() =12,
=12,
∴S△ABC=![]() ×BC×AD=
×BC×AD=![]() ×AB×CN,
×AB×CN,
∴CN=![]() =
=![]() ,
,
∵E关于AD的对称点M,
∴EP=PM,
∴CP+EP=CP+PM=CM,
根据垂线段最短得出:CM≥CN,
即CP+EP≥![]() ,
,
即CP+EP的最小值是![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你知道距离地面5千米的高空温度是多少吗?
(4)你能猜出距离地面6千米的高空温度是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,小明同爸爸妈妈一起从焦作出发去南阳看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小明一家这次行程中距姥姥家的距离 y(千米)与他们路途所用的时间 x(时)之间的函数图象,请根据以上信息,解答下列问题:
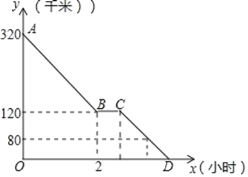
(1)求直线 AB 所对应的函数关系式;
(2)已知小明一家出服务区后,行驶 30 分钟时,距姥姥家还有 80 千米,问:若小明一家 当天早上 7 点从焦作出发,那么他们几点到达姥姥家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,2),B(4,3),C(1,1).

(1)在图中作出△ABC关于y轴对称的△![]()
![]()
![]() ;
;
(2)写出点△![]() ,
,![]() ,
,![]() 的坐标(直接写答案):
的坐标(直接写答案): ![]() ___;
___;![]() ___;
___;![]() ___;
___;
(3)△![]()
![]()
![]() 的面积为___;
的面积为___;
(4)在y轴上画出点P,使PB+PC最小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
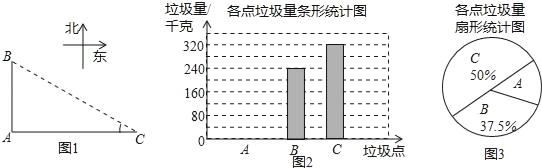
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图①,一条笔直的公路上有A、B、C三地,B.C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图像进行以下探究:

(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图像,求甲车到A地的距离y1与行驶时间x的函数表达式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com