
【题目】为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
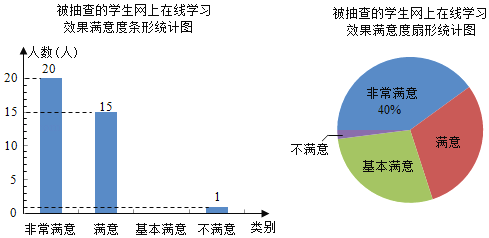
请根据图中信息解答下列问题:
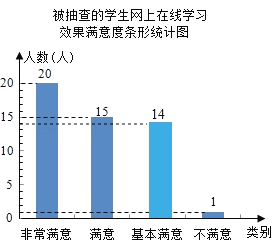
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
【答案】(1)50人,条形图见解析;(2)108°;(3)700
【解析】
(1)从两个统计图中可知,在抽查人数中,“非常满意”的人数为20人,占调查人数的40%,可求出调查人数,进而求出“基本满意”的人数,即可补全条形统计图;
(2)样本中“满意”占调查人数的![]() ,即30%,因此相应的圆心角的度数为360°的30%;
,即30%,因此相应的圆心角的度数为360°的30%;
(3)样本中“非常满意”或“满意”的占调查人数的(![]() ),进而估计总体中“非常满意”或“满意”的人数.
),进而估计总体中“非常满意”或“满意”的人数.
解:(1)抽查的学生数:20÷40%=50(人),
抽查人数中“基本满意”人数:50﹣20﹣15﹣1=14(人),补全的条形统计图如图所示:
(2)360°×![]() =108°,
=108°,
答:扇形统计图中表示“满意”的扇形的圆心角度数为108°;
(3)1000×![]() =700(人),
=700(人),
答:该校共有1000名学生中“非常满意”或“满意”的约有700人.


科目:初中数学 来源: 题型:
【题目】几何探究:
(问题发现)
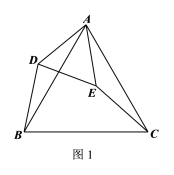
(1)如图1所示,△ABC和△ADE是有公共顶点的等边三角形,BD、CE的关系是_______(选填“相等”或“不相等”);(请直接写出答案)
(类比探究)
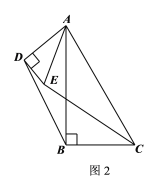
(2)如图2所示,△ABC和△ADE是有公共顶点的含有![]() 角的直角三角形,(1)中的结论还成立吗?请说明理由;
角的直角三角形,(1)中的结论还成立吗?请说明理由;
(拓展延伸)
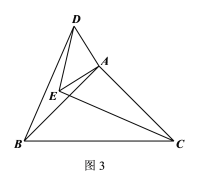
(3)如图3所示,△ADE和△ABC是有公共顶点且相似比为1 : 2的两个等腰直角三角形,将△ADE绕点A自由旋转,若![]() ,当B、D、E三点共线时,直接写出BD的长.
,当B、D、E三点共线时,直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。
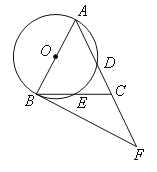
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
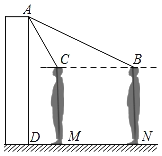
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
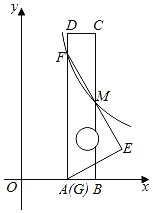
【题目】如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=![]() (x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=
(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG=![]() ,则k=_____.
,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
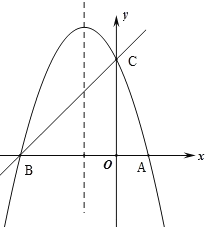
【题目】如图,已知抛物线![]() (a≠0)的对称轴为直线
(a≠0)的对称轴为直线![]() ,且抛物线经过A(1,0),C(0,3)两点,与
,且抛物线经过A(1,0),C(0,3)两点,与![]() 轴交于点B.
轴交于点B.
(1)若直线![]() 经过B,C两点,求直线BC和抛物线的解析式;
经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点M,使MA+MC的值最小,求点M的坐标;
上找一点M,使MA+MC的值最小,求点M的坐标;
(3)设P为抛物线的对称轴![]() 上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
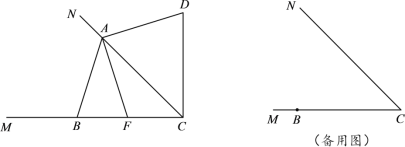
【题目】已知∠MCN=45°,点B在射线CM上,点A是射线CN上的一个动点(不与点C重合).点B关于CN的对称点为点D,连接AB、AD和CD,点F在直线BC上,且满足AF⊥AD.小明在探究图形运动的过程中发现AF=AB:始终成立.
![]() 如图,当0°<∠BAC<90°时.
如图,当0°<∠BAC<90°时.
① 求证:AF=AB;
② 用等式表示线段![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
![]() 当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com