
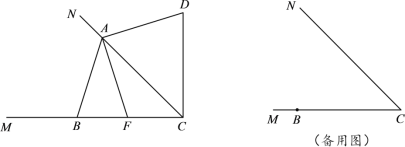
【题目】已知∠MCN=45°,点B在射线CM上,点A是射线CN上的一个动点(不与点C重合).点B关于CN的对称点为点D,连接AB、AD和CD,点F在直线BC上,且满足AF⊥AD.小明在探究图形运动的过程中发现AF=AB:始终成立.
![]() 如图,当0°<∠BAC<90°时.
如图,当0°<∠BAC<90°时.
① 求证:AF=AB;
② 用等式表示线段![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
![]() 当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
【答案】![]() ①证明过程见解析,②CD+CF=
①证明过程见解析,②CD+CF=![]() AC,过程见解析;
AC,过程见解析;![]()
![]() .
.
【解析】
![]() ①过点A作AG⊥BC于G,作AH⊥CD于H,判断出四边形AGCH是矩形,得出∠GAH=90°,得出∠FAG=∠DAH,进而判断出△FAG≌△DAH,即可得出结论; ②由矩形AGCH是正方形,判断出CH=CG,∠CAH=∠DCA=45°,由①知,△AGF≌△AHD,得出FG=DH,即CH=
①过点A作AG⊥BC于G,作AH⊥CD于H,判断出四边形AGCH是矩形,得出∠GAH=90°,得出∠FAG=∠DAH,进而判断出△FAG≌△DAH,即可得出结论; ②由矩形AGCH是正方形,判断出CH=CG,∠CAH=∠DCA=45°,由①知,△AGF≌△AHD,得出FG=DH,即CH=![]() ,再根据勾股定理得,AC=
,再根据勾股定理得,AC= ![]() CH,即可得出结论;
CH,即可得出结论;
![]() 同(1)的方法判断出△AHD≌AGF,得出DH=FG,进而得出CH=
同(1)的方法判断出△AHD≌AGF,得出DH=FG,进而得出CH=![]() ,即可得出结论.
,即可得出结论.
解:(1)①如图1, ∵点D,B关于CD对称,
∴AB=AD,∠BAC=∠DAC,∠ACD=∠MCN=45°,
∴∠DCM=90°,
过点A作AG⊥BC于G,作AH⊥CD于H,
∴AG=AH,∠AGC=∠AHC=∠DCM=90°,
∴四边形AGCH是矩形,
∴∠GAH=90°,
∵AF⊥AD,
∴∠FAD=90°,
∴∠FAG=∠DAH,
∴△AGF≌△AHD(ASA),
∴AF=AD,
∵AB=AD,
∴AF=AB;
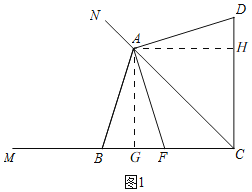
②结论:CD+CF=![]() AC, 理由:由①知,四边形AGCH是矩形,AG=AH,
AC, 理由:由①知,四边形AGCH是矩形,AG=AH,
∴矩形AGCH是正方形,
∴CH=CG,∠CAH=∠DCA=45°,
由①知,△AGF≌△AHD,
∴FG=DH,
∴CD+CF=CH+DH+CG-FG=2CH,
∴CH=![]() ,
,
根据勾股定理得,AC=![]() CH=
CH=![]() ,
,
∴CD+CF=![]() ;
;
(2)结论:CD-CF=![]() AC, 理由:如备用图, 同(1)的方法得,△AHD≌AGF,
AC, 理由:如备用图, 同(1)的方法得,△AHD≌AGF,

∴DH=FG,
∴CD-CF=CH+DH-FG+CG=2CH,
∴CH=![]() ,
,
根据勾股定理得,AC=![]() CH=
CH=![]() ,
,
∴CD-CF=![]() AC,
AC,
故答案为:CD-CF=![]() AC.
AC.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
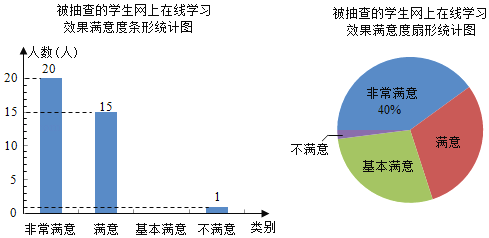
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
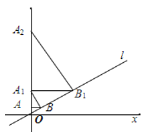
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
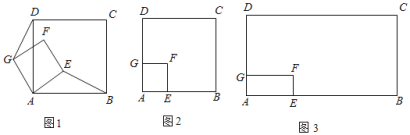
【题目】(1)问题探究:如图1所示,有公共顶点A的两个正方形ABCD和正方形AEFG.AE<AB,连接BE与DG,请判断线段BE与线段DG之间有怎样的数量关系和位置关系.并请说明理由.
(2)理解应用:如图2所示,有公共顶点A的两个正方形ABCD和正方形AEFG,AE<AB,AB=10,将正方形AEFG绕点A在平面内任意旋转,当∠ABE=15°,且点D、E、G三点在同一条直线上时,请直接写出AE的长 ;
(3)拓展应用:如图3所示,有公共顶点A的两个矩形ABCD和矩形AEFG,AD=4![]() ,AB=4
,AB=4![]() ,AG=4,AE=4
,AG=4,AE=4![]() ,将矩形AEFG绕点A在平面内任意旋转,连接BD,DE,点M,N分别是BD,DE的中点,连接MN,当点D、E、G三点在同一条直线上时,请直接写出MN的长
,将矩形AEFG绕点A在平面内任意旋转,连接BD,DE,点M,N分别是BD,DE的中点,连接MN,当点D、E、G三点在同一条直线上时,请直接写出MN的长
查看答案和解析>>
科目:初中数学 来源: 题型:
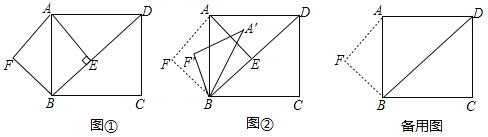
【题目】已知:如图①,在矩形![]() 中,
中,![]() ,垂足是
,垂足是![]() .点
.点![]() 是点
是点![]() 关于
关于![]() 的对称点,连接
的对称点,连接![]()
![]() .
.
(1)求![]() 和
和![]() 的长;
的长;
(2)若将![]() 沿着射线
沿着射线![]() 方向平移,设平移的距离为
方向平移,设平移的距离为![]() (平移距离指点
(平移距离指点![]() 沿
沿![]() 方向所经过的线段长度).当点
方向所经过的线段长度).当点![]() 分别平移到线段
分别平移到线段![]() 上时,直接写出相应的
上时,直接写出相应的![]() 的值.
的值.
(3)如图②,将![]() 绕点
绕点![]() 顺时针旋转一个角
顺时针旋转一个角![]() ,记旋转中
,记旋转中![]() 为
为![]() ,在旋转过程中,设
,在旋转过程中,设![]() 所在的直线与直线
所在的直线与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .是否存在这样的
.是否存在这样的![]() 两点,使
两点,使![]() 为等腰三角形?若存在,求出此时
为等腰三角形?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
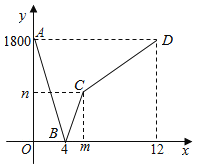
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的阻离为
(小时),两车之间的阻离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 之间的函数关系,则图中
之间的函数关系,则图中![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
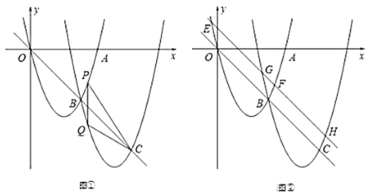
【题目】如图①,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移
先向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() (含端点)间的一点,作
(含端点)间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连按
,连按![]() ,
,![]() .当
.当![]() 的面积为
的面积为![]() 时, 求点
时, 求点![]() 的坐标;
的坐标;
(3)如图②,将直线![]() 向上平移,交抛物线
向上平移,交抛物线![]() 于点
于点![]() 、
、![]() ,交抛物线
,交抛物线![]() 于点
于点![]() 、
、![]() ,试判断
,试判断![]() 的值是否为定值,并说明理由.
的值是否为定值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .有下列结论:
.有下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④若点
;④若点![]() ,
,![]() 在抛物线上,则
在抛物线上,则![]() .其中正确结论的个数是()
.其中正确结论的个数是()
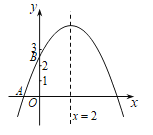
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
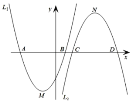
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com