
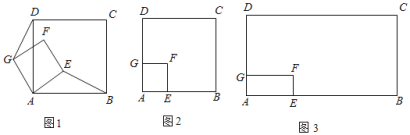
����Ŀ����1������̽������ͼ1��ʾ���й�������A������������ABCD��������AEFG��AE��AB������BE��DG�����ж��߶�BE���߶�DG֮����������������ϵ��λ�ù�ϵ������˵�����ɣ�
��2������Ӧ�ã���ͼ2��ʾ���й�������A������������ABCD��������AEFG��AE��AB��AB��10����������AEFG�Ƶ�A��ƽ����������ת������ABE��15�����ҵ�D��E��G������ͬһ��ֱ����ʱ����ֱ��д��AE�ij��� ����
��3����չӦ�ã���ͼ3��ʾ���й�������A����������ABCD�;���AEFG��AD��4![]() ��AB��4
��AB��4![]() ��AG��4��AE��4
��AG��4��AE��4![]() ��������AEFG�Ƶ�A��ƽ����������ת������BD��DE����M��N�ֱ���BD��DE���е㣬����MN������D��E��G������ͬһ��ֱ����ʱ����ֱ��д��MN�ij��� ��
��������AEFG�Ƶ�A��ƽ����������ת������BD��DE����M��N�ֱ���BD��DE���е㣬����MN������D��E��G������ͬһ��ֱ����ʱ����ֱ��д��MN�ij��� ��
���𰸡���1��BE��DG��BE��DG������������2��5![]() ��5����3��6
��5����3��6![]() ��8
��8![]()
��������
��1���ɡ�SAS����֤��GAD�ա�EAB���ɵ�BE��DG����ADG����ABE����ֱ�������ε����ʿɵ�BE��DG��
��2���ɡ�SAS����֤��GAD�ա�EAB���ɵ�BE��DG����ADG����ABE��15�㣬�ɵá�DEB��90�㣬��ֱ�������ε����ʿ���⣻
��3��������������ۣ�ͨ��֤����AGD�ס�AEB���ɵ�![]() ����DGA����AEB���ɹ��ɶ�������������λ�߶�������⣮
����DGA����AEB���ɹ��ɶ�������������λ�߶�������⣮
�⣺��1��BE��DG��BE��DG��
�������£���ͼ1���ӳ�BE��AD��N����DG��H��

���ı���ABCD�������Σ��ı���AEFG�������Σ�
��AG��AE��AB��AD����GAE����DAB��90�㣬
���GAD����EAB��
���GAD�ա�EAB��SAS����
��BE��DG����ADG����ABE��
�ߡ�ABE+��ANB��90�㣬
���ADG+��DNH��90�㣬
���DHN��90�㣬
��BE��DG��
��2����ͼ������G���߶�DE��ʱ������BD��

���ı���ABCD�������Σ��ı���AEFG�������Σ�
��AG��AE��AB��AD��10����GAE����DAB��90�㣬��ADB��45�㣽��ABD��BD��![]() AB��10
AB��10![]() ��GE��
��GE��![]() AE��
AE��
���GAD����EAB��
���GAD�ա�EAB��SAS����
��BE��DG����ADG����ABE��15�㣬
���BDE��45�㩁15�㣽30�㣬��DBE��45��+15�㣽60�㣬
���DEB��90�㣬
��BE��![]() BD��5
BD��5![]() ��DG��DE��
��DG��DE��![]() BE��5
BE��5![]() ��
��
��GE��5![]() ��5
��5![]() ��
��
��AE��![]() ��5
��5![]() ��5��
��5��
����E���߶�DG��ʱ��

ͬ������AE��5![]() ��5��
��5��
�ʴ�Ϊ��5![]() ��5��
��5��
��3����ͼ������G���߶�DE��ʱ��

��AD��4![]() ��AB��4
��AB��4![]() ��AG��4��AE��4
��AG��4��AE��4![]() ��
��
��DB��![]() ��
��![]() ��8
��8![]() ��GE��
��GE��![]() ��
��![]() ��8����DAB����GAE��90�㣬
��8����DAB����GAE��90�㣬
���DAG����BAE��
�֡�![]() ��
��
���AGD�ס�AEB��
��![]() ����DGA����AEB��
����DGA����AEB��
��BE��![]() DG��
DG��
�ߡ�DGA����GAE+��DEA����AEB����DEB+��AED��
���GAE����DEB��90�㣬
��DB2��DE2+BE2��
��64��13����DG+8��2+3DG2��
��DG��12��DG����16����ȥ����
��BE��12![]() ��
��
�ߵ�M��N�ֱ���BD��DE���е㣬
��MN��![]() BE��6
BE��6![]() ��
��
��ͼ������E���߶�DG��ʱ��

ͬ������BE��16![]() ��
��
�ߵ�M��N�ֱ���BD��DE���е㣬
��MN��![]() BE��8
BE��8![]() ��
��
����������MNΪ6![]() ��8
��8![]() ��
��
�ʴ�Ϊ��6![]() ��8
��8![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
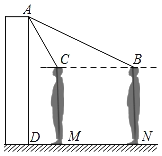
����Ŀ��ijУΪ���ʦ�����£���У�Ű�װ��ij�ͺŲ����ţ���ͼΪ�ò����Ž���ʾ��ͼ����֪������AD�Ķ���A��������Ϊ2.2m��Ϊ�˽��Լ�����Ч�������䣮����1.6m��С����������ʵ�飺�����ڵ���N��ʱ�����ſ�ʼ��ʾ��ͷ�¶ȣ���ʱ�ڶ�ͷB�����A������Ϊ18�����ڵ���M��ʱ��������ֹͣ��ʾ��ͷ�¶ȣ���ʱ�ڶ�ͷC�����A������Ϊ60������С���ڵ������Ч��������MN�ij��ȣ�����ͷ������ľ��������ƣ����㾫ȷ��0.1m��sin18���0.31��cos18���0.95��tan18���0.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
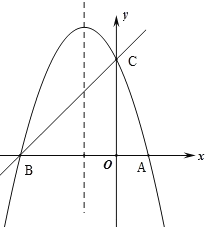
����Ŀ����ͼ����֪������![]() (a��0)�ĶԳ���Ϊֱ��
(a��0)�ĶԳ���Ϊֱ��![]() ���������߾���A(1��0)��C(0��3)���㣬��
���������߾���A(1��0)��C(0��3)���㣬��![]() �ύ�ڵ�B��
�ύ�ڵ�B��
��1����ֱ��![]() ����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���![]() ����һ��M��ʹMA+MC��ֵ��С�����M�����ꣻ
����һ��M��ʹMA+MC��ֵ��С�����M�����ꣻ
��3����PΪ�����ߵĶԳ���![]() �ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
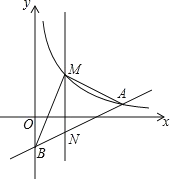
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(8��1)��B(0��3)������������![]() (x>0)��ͼ����A����ֱ��x=t(0<t<8)�뷴����������ͼ���ڵ�M����ֱ��AB���ڵ�N.
(x>0)��ͼ����A����ֱ��x=t(0<t<8)�뷴����������ͼ���ڵ�M����ֱ��AB���ڵ�N.
(1)��k��ֵ��
(2)����BMN��������ֵ��
(3)��MA��AB����t��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У���A��45��������BD����BD��AD����E����F�ֱ���AB��CD�ϵĵ㣬����EF��BD�ڵ�O����EF��CD��BE��DF��1��
��1����EF�ij���
��2��ֱ��д��ABCD������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ɽʤ����˾������һ���µĴ�����Ʒ��ÿ������Ʒ����ɱ�Ϊ18Ԫ���������̷��֣�ÿ������![]() ���
���![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���
֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���![]() ��
��
![]() д����˾ÿ�µ�����
д����˾ÿ�µ�����![]() ��Ԫ
��Ԫ![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮�亯������ʽ��
֮�亯������ʽ��
![]() �����۵���Ϊ����Ԫʱ����˾ÿ���ܹ�������������������Ƕ��٣�
�����۵���Ϊ����Ԫʱ����˾ÿ���ܹ�������������������Ƕ��٣�
![]() ���ݹ��̲��Ź涨�����ּ���Ʒ�����۵��۲��ø���32Ԫ
���ݹ��̲��Ź涨�����ּ���Ʒ�����۵��۲��ø���32Ԫ![]() �����˾Ҫ���ÿ�²�����350��Ԫ��������ô�������ּ���Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
�����˾Ҫ���ÿ�²�����350��Ԫ��������ô�������ּ���Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
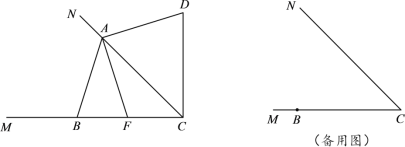
����Ŀ����֪��MCN��45������B������CM�ϣ���A������CN�ϵ�һ�����㣨�����C�غϣ�����B����CN�ĶԳƵ�Ϊ��D������AB��AD��CD����F��ֱ��BC�ϣ�������AF��AD��С����̽��ͼ���˶��Ĺ����з���AF��AB��ʼ�ճ�����
![]() ��ͼ����0������BAC��90��ʱ��
��ͼ����0������BAC��90��ʱ��
�� ��֤��AF��AB��
�� �õ�ʽ��ʾ�߶�![]() ��
��![]() ֮���������ϵ����֤����
֮���������ϵ����֤����
![]() ��90������BAC��135��ʱ��ֱ���õ�ʽ��ʾ�߶�CF��CD��CA֮���������ϵ�� ��
��90������BAC��135��ʱ��ֱ���õ�ʽ��ʾ�߶�CF��CD��CA֮���������ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�꼶����150��Ů����Ϊ�˽��УŮ��ʵ����ɼ�����λ���ף���������������λ����������������������ȡ30��Ů�����в��ԣ���������ǵ���سɼ����������ݽ��������������ͷ�������������˲�����Ϣ��
![]() ��ʵ����ɼ���Ƶ���ֲ������£�
��ʵ����ɼ���Ƶ���ֲ������£�
���� | 6��2�� | 6��6�� | 7��0�� | 7��4�� | 7��8�� | 8��2�� |
Ƶ�� | 2 |
| 10 | 6 | 2 | 1 |
![]() ��ʵ����ɼ���7��0��
��ʵ����ɼ���7��0��![]() ��7��4��������ǣ�
��7��4��������ǣ�
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
![]() ��һ�������������ɼ���ͼ��ʾ��
��һ�������������ɼ���ͼ��ʾ��

����������Ϣ���ش��������⣺
��1���ٱ���m��ֵΪ ��
�ڳ�ȡѧ��һ�������������ɼ�����λ��Ϊ ����
��2����ʵ����ɼ��ﵽ7��2�����ϣ��ɼ���Ϊ���㣬�����ȫ�꼶Ů���ɼ��ﵽ�����������
��3�����꼶ij������ίԱ����������γ��������б���ȡ��8��Ů��������ɼ������ݳ�¼���£�
������ | A | B | C | D | E | F | G | H |
ʵ���� | 8��1 | 7��7 | 7��5 | 7��5 | 7��3 | 7��2 | 7��0 | 6��5 |
һ������������ | * | 42 | 47 | * | 47 | 52 | * | 49 |
������2��Ů����һ�������������ɼ�δ��¼����������ʦ˵��8��Ů��ǡ����4��������Գɼ����ﵽ�����㣬��������ίԱ�Ʋ�Ů��E��һ�������������ɼ��ﵽ�����㣬��ͬ������ίԱ��˵���𣿲�˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]()
![]() ����
����![]() ������
������![]() �ڵ������ޣ�
�ڵ������ޣ�![]() ��
��![]() �������ߵĶԳ���
�������ߵĶԳ���![]() �ϵ����㣬��
�ϵ����㣬��![]() ����ֱ��
����ֱ��![]() �����
�����![]() ����������
����������![]() ����
����![]() ǡ�����������ϣ�
ǡ�����������ϣ�
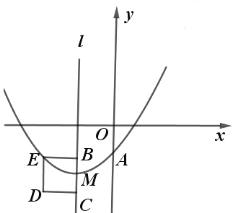
��1���ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��
��
��2����֤����![]() �͵�
�͵�![]() ����ֱ��
����ֱ��![]() �Գƣ�
�Գƣ�
��3���ж�ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �dz�������
�dz�������![]() ���Ľ����Ƿ����������ϣ���˵�����ɣ�
���Ľ����Ƿ����������ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com