
【题目】某年级共有150名女生,为了解该校女生实心球成绩(单位:米)和仰卧起坐(单位:个)的情况,从中随机抽取30名女生进行测试,获得了她们的相关成绩,并对数据进行整理、描述和分析,下面给出了部分信息.
![]() .实心球成绩的频数分布表如下:
.实心球成绩的频数分布表如下:
分组 | 6.2≤ | 6.6≤ | 7.0≤ | 7.4≤ | 7.8≤ | 8.2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
![]() .实心球成绩在7.0≤
.实心球成绩在7.0≤![]() <7.4.这组的是:
<7.4.这组的是:
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
![]() .一分钟仰卧起坐成绩如图所示:
.一分钟仰卧起坐成绩如图所示:

根据以上信息,回答下列问题:
(1)①表中m的值为 ;
②抽取学生一分钟仰卧起坐成绩的中位数为 个;
(2)若实心球成绩达到7.2米及以上,成绩记为优秀,请估计全年级女生成绩达到优秀的人数.
(3)该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整,当老师说这8名女生恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
【答案】(1)①9;②45;(2)65人;(3)同意,理由见解析
【解析】
(1)①根据题意和表格中的数据可以求得m的值;
②根据条形统计图中数据和中位数的定义可以得到这组数据的中位数;
(2)根据题意和表格中的数据可以求得全年级女生实心球成绩达到优秀的人数;
(3)根据题意和表格中的数据可以解答本题.
解:(1)①m=30-2-10-6-2-1=9,
故答案为:9;
②由条形统计图可得,一分钟仰卧起坐成绩的中位数为45,
故答案为:45;
(2)![]() (人)
(人)
答:全年级女生实心球成绩达到优秀的约有65人.
(3)同意.
理由答案不唯一,如果女生![]() 的仰卧起坐成绩未达到优秀,那么只有
的仰卧起坐成绩未达到优秀,那么只有![]() 、
、![]() 、
、![]() 有可能两项测试成绩都达到优秀,这与恰有4人两项测试成绩都达到优秀矛盾,因此女生
有可能两项测试成绩都达到优秀,这与恰有4人两项测试成绩都达到优秀矛盾,因此女生![]() 的一分钟仰卧起坐成绩达到了优秀.
的一分钟仰卧起坐成绩达到了优秀.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
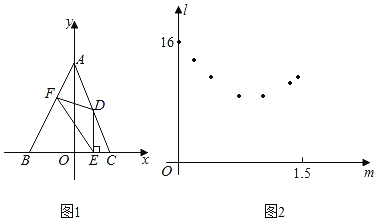
【题目】如图1,在平面直角坐标系中,△ABC的顶点A,C分別是直线y=﹣![]() x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
x+4与坐标轴的交点,点B的坐标为(﹣2,0),点D是边AC上的一点,DE⊥BC于点E,点F在边AB上,且D,F两点关于y轴上的某点成中心对称,连结DF,EF.设点D的横坐标为m,EF2为l,请探究:
①线段EF长度是否有最小值.
②△BEF能否成为直角三角形.
小明尝试用“观察﹣猜想﹣验证﹣应用”的方法进行探究,请你一起来解决问题.
(1)小明利用“几何画板”软件进行观察,测量,得到l随m变化的一组对应值,并在平面直角坐标系中以各对应值为坐标描点(如图2).请你在图2中连线,观察图象特征并猜想l与m可能满足的函数类别.
(2)小明结合图1,发现应用三角形和函数知识能验证(1)中的猜想,请你求出l关于m的函数表达式及自变量的取值范围,并求出线段EF长度的最小值.
(3)小明通过观察,推理,发现△BEF能成为直角三角形,请你求出当△BEF为直角三角形时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
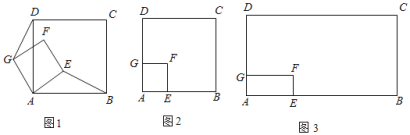
【题目】(1)问题探究:如图1所示,有公共顶点A的两个正方形ABCD和正方形AEFG.AE<AB,连接BE与DG,请判断线段BE与线段DG之间有怎样的数量关系和位置关系.并请说明理由.
(2)理解应用:如图2所示,有公共顶点A的两个正方形ABCD和正方形AEFG,AE<AB,AB=10,将正方形AEFG绕点A在平面内任意旋转,当∠ABE=15°,且点D、E、G三点在同一条直线上时,请直接写出AE的长 ;
(3)拓展应用:如图3所示,有公共顶点A的两个矩形ABCD和矩形AEFG,AD=4![]() ,AB=4
,AB=4![]() ,AG=4,AE=4
,AG=4,AE=4![]() ,将矩形AEFG绕点A在平面内任意旋转,连接BD,DE,点M,N分别是BD,DE的中点,连接MN,当点D、E、G三点在同一条直线上时,请直接写出MN的长
,将矩形AEFG绕点A在平面内任意旋转,连接BD,DE,点M,N分别是BD,DE的中点,连接MN,当点D、E、G三点在同一条直线上时,请直接写出MN的长
查看答案和解析>>
科目:初中数学 来源: 题型:
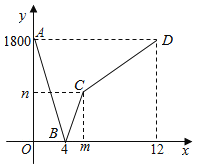
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的阻离为
(小时),两车之间的阻离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 之间的函数关系,则图中
之间的函数关系,则图中![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移
先向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
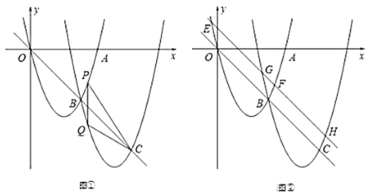
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() (含端点)间的一点,作
(含端点)间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连按
,连按![]() ,
,![]() .当
.当![]() 的面积为
的面积为![]() 时, 求点
时, 求点![]() 的坐标;
的坐标;
(3)如图②,将直线![]() 向上平移,交抛物线
向上平移,交抛物线![]() 于点
于点![]() 、
、![]() ,交抛物线
,交抛物线![]() 于点
于点![]() 、
、![]() ,试判断
,试判断![]() 的值是否为定值,并说明理由.
的值是否为定值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .有下列结论:
.有下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④若点
;④若点![]() ,
,![]() 在抛物线上,则
在抛物线上,则![]() .其中正确结论的个数是()
.其中正确结论的个数是()
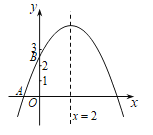
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
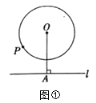
(1)如图①,已知![]() 与直线
与直线![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,则圆上一点
,则圆上一点![]() 到
到![]() 的距离的最小值是______;
的距离的最小值是______;
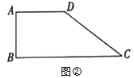
(2)如图②,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作一条直线交边
作一条直线交边![]() 或
或![]() 于
于![]() ,若
,若![]() 平分四边形
平分四边形![]() 的面积,求
的面积,求![]() 的长;
的长;
问题解决
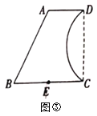
(3)如图③所示,是由线段![]() 、
、![]() 、
、![]() 与弧
与弧![]() 围成的花园的平面示意图,
围成的花园的平面示意图,![]() ,
,![]() ,
,![]() //
//![]() ,CD⊥BC,点
,CD⊥BC,点![]() 为
为![]() 的中点,
的中点,![]() 所对的圆心角为
所对的圆心角为![]() .管理人员想在
.管理人员想在![]() 上确定一点
上确定一点![]() ,在四边形
,在四边形![]() 区域种植花卉,其余区域种植草坪,并过
区域种植花卉,其余区域种植草坪,并过![]() 点修建一条小路
点修建一条小路![]() ,把四边形
,把四边形![]() 分成面积相等且尽可能小的两部分,分别种植不同的花卉.问是否存在满足上述条件的小路
分成面积相等且尽可能小的两部分,分别种植不同的花卉.问是否存在满足上述条件的小路![]() ?若存在,请求出
?若存在,请求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]()
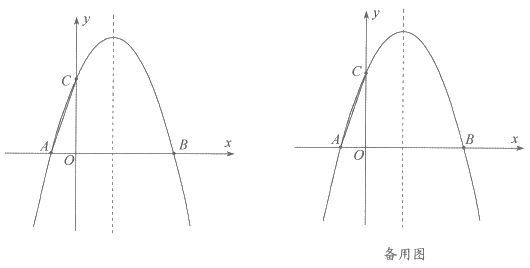
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴右侧抛物线图像上的一动点,设点
轴右侧抛物线图像上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①是否存在这样的点![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②若该动点![]() 在第一象限内,连接
在第一象限内,连接![]() ,当
,当![]() 时,求
时,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com