
【题目】已知:如图①,在矩形![]() 中,
中,![]() ,垂足是
,垂足是![]() .点
.点![]() 是点
是点![]() 关于
关于![]() 的对称点,连接
的对称点,连接![]()
![]() .
.
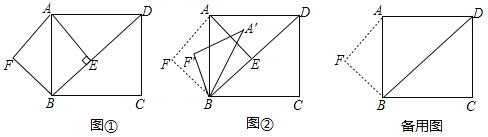
(1)求![]() 和
和![]() 的长;
的长;
(2)若将![]() 沿着射线
沿着射线![]() 方向平移,设平移的距离为
方向平移,设平移的距离为![]() (平移距离指点
(平移距离指点![]() 沿
沿![]() 方向所经过的线段长度).当点
方向所经过的线段长度).当点![]() 分别平移到线段
分别平移到线段![]() 上时,直接写出相应的
上时,直接写出相应的![]() 的值.
的值.
(3)如图②,将![]() 绕点
绕点![]() 顺时针旋转一个角
顺时针旋转一个角![]() ,记旋转中
,记旋转中![]() 为
为![]() ,在旋转过程中,设
,在旋转过程中,设![]() 所在的直线与直线
所在的直线与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .是否存在这样的
.是否存在这样的![]() 两点,使
两点,使![]() 为等腰三角形?若存在,求出此时
为等腰三角形?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在
;(3)存在![]() 组符合条件的点
组符合条件的点![]() 、点
、点![]() ,使
,使![]() 为等腰三角形;
为等腰三角形; ![]() 的长度分别为
的长度分别为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用矩形性质、勾股定理及三角形面积公式求解;
(2)依题意画出图形,如图①-1所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;
(3)在旋转过程中,等腰△DPQ有4种情形,分别画出图形,对于各种情形分别进行计算即可.
(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
在Rt△ABD中,AB=3,AD=4,
由勾股定理得:BD=![]() ,
,
∵S△ABD![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=![]() ,
,
∵点F是点E关于AB的对称点,
∴AF=AE![]() ,BF=BE,
,BF=BE,
∵AE⊥BD,
∴∠AEB=90°,
在Rt△ABE中,AB=3,AE![]() ,
,
由勾股定理得:BE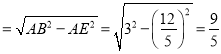 ;
;
(2)设平移中的三角形为△A′B′F′,如图①-1所示:
由对称点性质可知,∠1=∠2.BF=BE![]() ,
,
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′![]() ,
,
①当点F′落在AB上时,
∵AB∥A′B′,
∴∠3=∠4,
根据平移的性质知:∠1=∠4,
∴∠3=∠2,
∴BB′=B′F′![]() ,即
,即![]() ;
;
②当点F′落在AD上时,
∵AB∥A′B′,AB⊥AD,
∴∠6=∠2,A′B′⊥AD,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又知A′B′⊥AD,
∴△B′F′D为等腰三角形,
∴B′D=B′F′![]() ,
,
∴BB′=BD-B′D=5-![]() ,即m
,即m![]() ;
;
(3)存在.理由如下:
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AE⊥BD,
∴∠AEB=90°,
∠2+∠ABD=90°,∠BAE+∠ABD=90°,
∴∠2=∠BAE,
∵点F是点E关于AB的对称点,
∴∠1=∠BAE,
∴∠1=∠2,
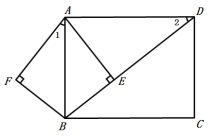
在旋转过程中,等腰△DPQ依次有以下4种情形:
①如图③-1所示,点Q落在BD延长线上,且PD=DQ,
则∠Q=∠DPQ,
∴∠2=∠Q+∠DPQ=2∠Q,
∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′B=3,
∴F′Q=F′A′+A′Q=![]() ,
,
在Rt△BF′Q中,由勾股定理得:BQ=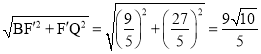 ,
,
∴DQ=BQ-BD=![]() ;
;
②如图③-2所示,点Q落在BD上,且PQ=DQ,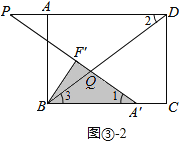
则∠2=∠P,
∵∠1=∠2,
∴∠1=∠P,
∴BA′∥PD,
则此时点A′落在BC边上.
∵∠3=∠2,
∴∠3=∠1,
∴BQ=A′Q,
∴F′Q=F′A′-A′Q=![]() -BQ,
-BQ,
在Rt△BQF′中,由勾股定理得:BF′2+F′Q2=BQ2,
即:![]() ,
,
解得:![]() ,
,
∴DQ= BD-BQ=5-![]() ;
;
③如图③-3所示,点Q落在BD上,且PD=DQ,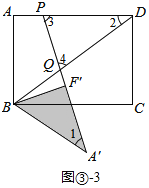
则∠3=∠4.
∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°-![]() ∠2.
∠2.
∵∠1=∠2,
∴∠4=90°-![]() ∠1,
∠1,
∴∠A′QB=∠4=90°-![]() ∠1,
∠1,
∴∠A′QB=∠A′BQ,
∴A′Q=A′B=3,
∴F′Q=A′Q-A′F′=3-![]() ,
,
在Rt△BF′Q中,由勾股定理得:BQ=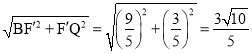 ,
,
∴DQ=BQ-BD=![]() ;
;
④如图④-4所示,点Q落在BD上,且PQ=PD,
则∠2=∠3.
∵∠1=∠2,∠3=∠4,∠2=∠3,
∴∠1=∠4,
∴BQ=BA′=3,
∴DQ=BD-BQ=5-3=2.
综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形,DQ的长度分别为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
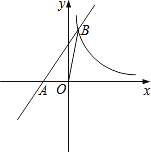
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 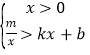 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,∠A=45°,连接BD,且BD⊥AD,点E、点F分别是AB、CD上的点,连接EF交BD于点O,且EF⊥CD,BE=DF=1.
(1)求EF的长;
(2)直接写出ABCD的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
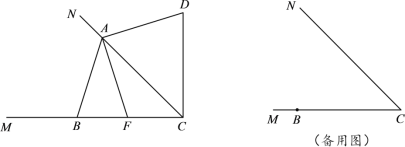
【题目】已知∠MCN=45°,点B在射线CM上,点A是射线CN上的一个动点(不与点C重合).点B关于CN的对称点为点D,连接AB、AD和CD,点F在直线BC上,且满足AF⊥AD.小明在探究图形运动的过程中发现AF=AB:始终成立.
![]() 如图,当0°<∠BAC<90°时.
如图,当0°<∠BAC<90°时.
① 求证:AF=AB;
② 用等式表示线段![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
![]() 当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
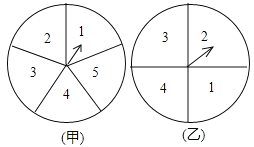
【题目】小明和小亮用如图所示的甲、乙两个转盘(甲转盘被分成五个面积相等的扇形,乙转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次(如果指针恰好在分割线上,那么重转一次,直到指针指向某一扇形区域为止).
(1)请你求出甲转盘指针指向偶数区域的概率;
(2)若两次数字之和为![]() ,
,![]() 或
或![]() 时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
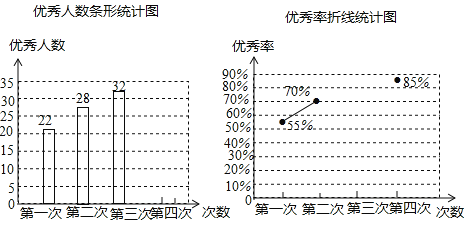
(1)求该班总人数;
(2)根据计算,请你补全两个统计图;
(3)已知该班甲同学四次训练成绩为85,95,85,95,乙同学四次成绩分别为85,90,95,90,现需从甲、乙两同学中选派一名同学参加校级比赛,你认为应该选派哪位同学并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年,我省中考体育分值增加到
年,我省中考体育分值增加到![]() 分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
百分比 |
|
|
|
|
|
(1)求样本容量及表格中的![]() 和
和![]() 的值
的值
(2)求扇形统计图中![]() 等级所对的圆心角度数,并补全统计图.
等级所对的圆心角度数,并补全统计图.
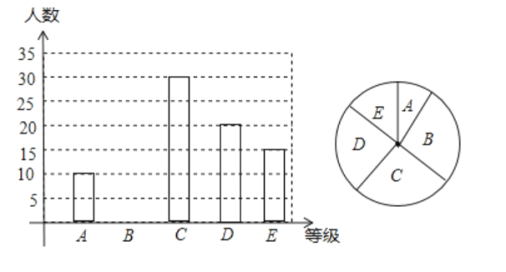
(3)我校![]() 年级共有女生
年级共有女生![]() 人.若女生八百米成绩的达标成绩为
人.若女生八百米成绩的达标成绩为![]() 分,我校九年级女生八百米成绩达标的人数有多少?
分,我校九年级女生八百米成绩达标的人数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com