
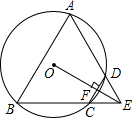
 如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.分析 (1)根据圆内接四边形的性质可得∠A+∠BCD=180°,根据邻补角互补可得∠DCE+∠BCD=180°,进而得到∠A=∠DCE,然后利用等边对等角可得∠DCE=∠AEB,进而可得∠A=∠AEB;
(2)首先证明△DCE是等边三角形,进而可得∠AEB=60°,再根据∠A=∠AEB,可得△ABE是等腰三角形,进而可得△ABE是等边三角形.
解答 证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB;
(2)∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
点评 此题主要考查了等边三角形的判定和性质,以及圆内接四边形的性质,关键是掌握圆内接四边形对角互补.


科目:初中数学 来源: 题型:选择题
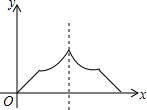 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周,设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
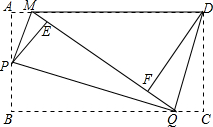 如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com