
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第![]() 天(
天(![]() 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
为整数)的售价、销量及储存和损耗费用的相关信息如表所示.
时间 |
|
|
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) |
|
|
储存和损耗费用(元) |
|
|
已知该种水果的进价为4.1元/斤,设销售该水果第![]() (天)的利润为
(天)的利润为![]() (元),求
(元),求![]() 与
与![]() (
(![]() )之间的函数解析式,并求出第几天时销售利润最大.
)之间的函数解析式,并求出第几天时销售利润最大.
【答案】(1)10%;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;第10天时销售利润最大
;第10天时销售利润最大
【解析】
(1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;
(2)根据两个取值先计算:当1≤x<9时和9≤x<15时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比.
(1)设该种水果每次降价的百分率是![]() ,依题意,得:
,依题意,得:
![]()
解得![]() 或
或![]() (不符合题意,舍去),
(不符合题意,舍去),
答:该种水果每次降价的百分率是10%;
(2)当![]() 时,第1次降价后的价格:
时,第1次降价后的价格:![]() 元,
元,
∴![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() (元),
(元),
当![]() 时,第2次降价后的价格:8.1元,
时,第2次降价后的价格:8.1元,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() (元)
(元)
∵380>334.3
∴第10天时销售利润最大;


科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
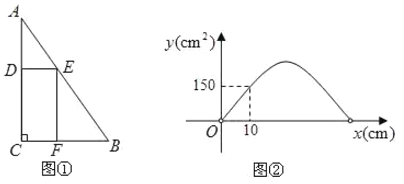
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
(3)若![]() 与
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
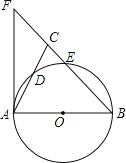
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是由四边形ABCD经过旋转得到的,如果用有序数对(3,1)表示方格纸上A点的位置,用(2,2)表示点B的位置,那么由四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示为_____(数为整数)
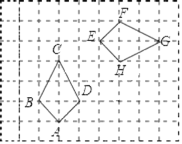
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
(1)求证:直线AB是⊙O的切线;
(2)OA,OB分别交⊙O于点D,E,AO的延长线交⊙O于点F,若AB=4AD,求sin∠CFE的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com