
 “锤子、剪刀、布”是一个古老的儿童游戏,三种不同手势分别代表锤子、剪刀、布.规则是:锤子胜剪刀,剪刀胜布,布胜锤子;当两人做出相同的手势时,不能决定胜负.设甲、乙两人都等可能地采取三种手势.
“锤子、剪刀、布”是一个古老的儿童游戏,三种不同手势分别代表锤子、剪刀、布.规则是:锤子胜剪刀,剪刀胜布,布胜锤子;当两人做出相同的手势时,不能决定胜负.设甲、乙两人都等可能地采取三种手势.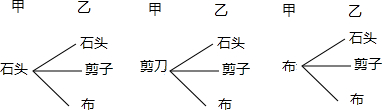
| 3 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 出行方式 | 坐公交车 | 骑自行车、电动车 | 开私家车 | 坐单位班车 |
| 人数 | 250 | 270 | 70 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
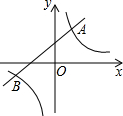 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
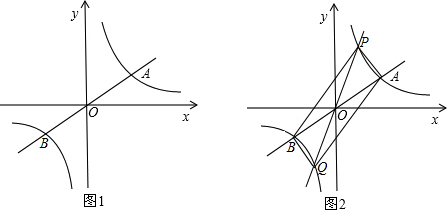
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
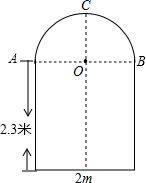 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com