
 有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.| A. | 64 | B. | 52 | C. | 38 | D. | 26 |
分析 连结OE、OD,如图,当点O、E、D共线时,半圆片上的点D与原点O距离最大,根据三角形外角性质得∠AED=∠EAO+∠EOA,再根据直角三角形斜边上的中线性质得EA=EO=EB,则∠EAO=∠EOA,所以n=$\frac{1}{2}$∠ADE=26°.
解答 解:连结OE、OD,如图,当点O、E、D共线时,半圆片上的点D与原点O距离最大,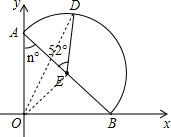
则∠AED=∠EAO+∠EOA,
而AE=BE,
所以EA=EO=EB,
所以∠EAO=∠EOA,
所以n=$\frac{1}{2}$∠ADE=26°.
故选D.
点评 本题考查了圆的认识:圆可以看做是所有到定点O的距离等于定长r的点的集合.掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | a+3>b+3 | B. | a-π>b-π | C. | ac2>bc2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
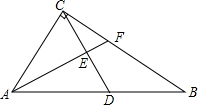 在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.
在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,四边形ABCD,连接AC,∠ABC=∠BAC=∠DAC=$\frac{1}{2}$∠ADC,若DC=2AD=4,则△ABC的面积为3$\sqrt{15}$.
已知,四边形ABCD,连接AC,∠ABC=∠BAC=∠DAC=$\frac{1}{2}$∠ADC,若DC=2AD=4,则△ABC的面积为3$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
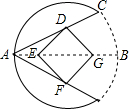 如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$.
如图,在圆的正中央摆放着一个正方形DEFG,且正方形的顶点D在弦AC上、对角线EG在直径AB上.若EG=4,AB=8,则AC=$\frac{16\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
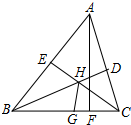 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com