

���� ��1����A��C��������������ʽ�������b��c��Ȼ��ó�����D�����꣬���ô���ϵ�������ֱ��AD����ʽ��
��2���ӳ�QN��x���ڵ�F������D��DE��x���ڵ�E������N��NG��QM��G�㣬���жϳ���QM���ʱ����QNM�ܳ���������Q��M�����꣬��϶��κ�����ɣ�
��3����4�����������ͼ��������λ�ߺ����Ƶ��й�֪ʶ���н�ɣ�
��� �⣺��1����A��-1��0���͵�C��0��3������y=-x2+bx+c���ã�
$\left\{\begin{array}{l}{-1-b+c=0}\\{c=3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-x2+2x+3��
�ඥ��D��1��4����
��ֱ��AD�Ľ���ʽΪ��y=kx+b��
��A��-1��0����D��1��4����ֱ��AD�ϣ��ã�
$\left\{\begin{array}{l}{-k+b=0}\\{k+b=4}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$��
��ֱ��AD�Ľ���ʽΪ��y=2x+2��
��2����ͼ1��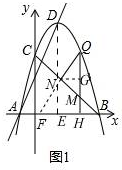
�ӳ�QN��x���ڵ�F������D��DE��x���ڵ�E��
����N��NG��QM��G�㣬
A��-1��0��B��3��0��C��0��3��D��1��4��
��QN��DA��
���QFH=��DAH��
�ߡ�DEA=��QHF=90�㣬
���ADE=��FQH��
��$tan��NQG=tan��ADE=\frac{AE}{DE}=\frac{2}{4}=\frac{1}{2}$��
��QH��CO��
���QMN=��OCB=45�㣬
��NG=x����GM=x��QG=2x��
��$NM=\sqrt{2}x$��$QN=\sqrt{5}x$��QM=3x��
��${C_{��QMN}}=��3+\sqrt{2}+\sqrt{5}��x$��
���Ե�xȡ���ֵʱ������QMȡ���ֵʱ����QNM���ܳ����
�����㷨����ֱ��BC��y=-x+3��
��Q��m��-m2+2m+3������M��m��-m+3��
$\begin{array}{l}QM=-{m^2}+2m+3-��-m+3��\\ \;\;\;\;\;\;\;=-{m^2}+3m\end{array}$
�൱$m=-\frac{1}{{2����-\frac{1}{3}��}}=\frac{3}{2}$ʱ��QMȡ���ֵΪ��$\frac{9}{4}$��
��ʱ��-m2+2m+3=$\frac{15}{4}$��
��ʱ$Q��\frac{3}{2}��\frac{15}{4}��$��
QM=3x=$\frac{9}{4}$��
����x=$\frac{3}{4}$��
��QNM�ܳ������ֵΪ��3x=��3+$\sqrt{2}$+$\sqrt{5}$����$\frac{3}{4}$=$\frac{9+3\sqrt{2}+3\sqrt{5}}{4}$��
��3������4�������
�١�FRP=90��ʱ����ͼ2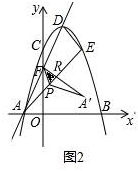
FA�佻AE�ڵ�R��
F��0��2��AF=$\sqrt{5}$=DF��
E��2��3����DE=$\sqrt{2}$��AD=$2\sqrt{5}$��$AE=3\sqrt{2}$��
��DE2+AE2=20=AD2��
���DEA=90�㣬
�ߡ�FRA=��DEA=90�㣬
��FR��DE��
��FΪDA�е㣬
��FRΪ��DAE��λ�ߣ�
��AR=$\frac{1}{2}AE=\frac{3}{2}\sqrt{2}$��FR=$\frac{1}{2}DE=\frac{{\sqrt{2}}}{2}$��
��P����PK��AF��K�㣬
�ڡ�PKF�͡�PRF��$\left\{\begin{array}{l}��PKF=��PRF={90��}\\��PFK=��PFR\\ PF=PF\end{array}\right.$��
���PKF�ա�PRF��
��PK=PR��FK=FR��
��PR=PK=x����PA=$\frac{{3\sqrt{2}}}{2}-x$��AK=AF-KF=$\sqrt{5}-\frac{{\sqrt{2}}}{2}$��
AK$\begin{array}{l}A{K^2}+P{K^2}=A{P^2}\\{��\sqrt{5}-\frac{{\sqrt{2}}}{2}��^2}+{x^2}={��\frac{{3\sqrt{2}}}{2}-x��^2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=\frac{{2\sqrt{5}-\sqrt{2}}}{6}\end{array}$��
��AP=$\frac{{3\sqrt{2}}}{2}-\frac{{2\sqrt{5}-\sqrt{2}}}{6}=\frac{{5\sqrt{2}-\sqrt{5}}}{3}$��
�ڡ�FPA'=90�㣬��ͼ3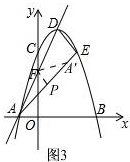
�ɢٿ�֪FPΪ��DAE��λ��
��AP=$\frac{1}{2}AE=\frac{3}{2}\sqrt{2}$��
�ۡ�PFA'=90�㣬��ͼ4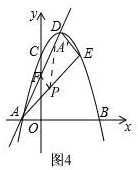
��FA=FD��PF��AD
��PFΪAD��ֱƽ����
��AP=DP
��AP=x����PE=$3\sqrt{2}-x$
$\begin{array}{l}P{E^2}+D{E^2}=P{D^2}\\{��3\sqrt{2}-x��^2}+2={x^2}\\ \;\;\;\;\;\;x=\frac{{5\sqrt{2}}}{3}\end{array}$
��$AP=\frac{{5\sqrt{2}}}{3}$
�ܡ�PK'F=90�㣬��ͼ5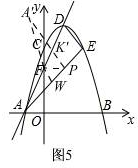
PA�佻AD�ڵ�K�䣬
����F��FW��AE�ڵ�W
�ɢٿ�֪��FW=$\frac{1}{2}DE=\frac{{\sqrt{2}}}{2}$
AW=$\frac{1}{2}AE=\frac{{3\sqrt{2}}}{2}$
�ߡ�WPF=��K'PF��FK'��PK'��FW��AP
��$FK'=FW=\frac{{\sqrt{2}}}{2}$
��PK'=PW
��$AK'=\sqrt{5}+\frac{{\sqrt{2}}}{2}$
��$\left\{\begin{array}{l}{��K��AP=��EAD}\\{��AK��P=��AED=90��}\end{array}\right.$��
���AK'P�ס�AED��
��$\begin{array}{l}\frac{AK'}{AE}=\frac{PK'}{DE}\\ \frac{{\sqrt{5}+\frac{{\sqrt{2}}}{2}}}{{3\sqrt{2}}}=\frac{PK'}{{\sqrt{2}}}\\ \;\;\;\;PK'=\frac{{2\sqrt{5}+\sqrt{2}}}{6}\end{array}$
��$PW=AK'=\frac{{2\sqrt{5}+\sqrt{2}}}{6}$
��$AP=AW+WP=\frac{{3\sqrt{2}}}{2}+\frac{{2\sqrt{5}+\sqrt{2}}}{6}=\frac{{5\sqrt{2}+\sqrt{5}}}{3}$
���ϣ�AP�ij���Ϊ$\frac{{5\sqrt{2}-\sqrt{5}}}{3}$��$\frac{{3\sqrt{2}}}{2}$��$\frac{{5\sqrt{2}}}{3}$��$\frac{{5\sqrt{2}+\sqrt{5}}}{3}$
���� ���⿼����κ������ۺ����⣬���������ߺ�ֱ�ߵĽ���ʽ���������������ε��ܳ�������⣬���������������ֱ�������εĶ���Ĵ����������ǽ���Ĺؼ���ע���3�ʣ��ڽ���Dz�Ҫ©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
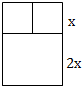 һ��ľ�ϳ�Ϊ42�ף�Ҫ��һ����ͼ�Ĵ�����֪�Ͽ�����¿�ܸߵı�Ϊ1��2����
һ��ľ�ϳ�Ϊ42�ף�Ҫ��һ����ͼ�Ĵ�����֪�Ͽ�����¿�ܸߵı�Ϊ1��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����O�İ뾶Ϊ1����ABC�ǡ�O���ڽӵȱ������Σ���D��E��Բ�ϣ��ı���BCDEΪ���Σ�������ε�����ǣ�������
��ͼ����O�İ뾶Ϊ1����ABC�ǡ�O���ڽӵȱ������Σ���D��E��Բ�ϣ��ı���BCDEΪ���Σ�������ε�����ǣ�������| A�� | 2 | B�� | $\sqrt{3}$ | C�� | 1 | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��һ��ԲƬ������Բ�Ľǡ�AED=52�㣩��ƽ��ֱ������ϵ�У�����ͼ��ʾ���ã�����A������y�����������»�����ͬʱ��B��Ӧ����x���������ϻ���������OAB=n��ʱ����ԲƬ�ϵĵ�D��ԭ��O���������nΪ���������㣮
��һ��ԲƬ������Բ�Ľǡ�AED=52�㣩��ƽ��ֱ������ϵ�У�����ͼ��ʾ���ã�����A������y�����������»�����ͬʱ��B��Ӧ����x���������ϻ���������OAB=n��ʱ����ԲƬ�ϵĵ�D��ԭ��O���������nΪ���������㣮| A�� | 64 | B�� | 52 | C�� | 38 | D�� | 26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ABC=90�㣬BDΪAC�����ߣ�����C��CE��BD�ڵ�E������A��BD��ƽ���ߣ���CE���ӳ����ڵ�F����AF���ӳ����Ͻ�ȡFG=BD������BG��DF����AF=12��CF=5�����ı���BDFG���ܳ���
��ͼ���ڡ�ABC�У���ABC=90�㣬BDΪAC�����ߣ�����C��CE��BD�ڵ�E������A��BD��ƽ���ߣ���CE���ӳ����ڵ�F����AF���ӳ����Ͻ�ȡFG=BD������BG��DF����AF=12��CF=5�����ı���BDFG���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | û��ʵ���� | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com