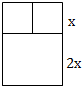Question

9．一根木料长为42米，要做一个如图的窗框，已知上框架与下框架高的比为1：2，求：
①窗框面积S与x的函数关系式；
②上、下框架的高各为多少时，能使光线通过的窗框面积最大？
③窗框最大面积．

Answer 1

分析 ①根据题意先表示出窗框的高为3x、宽为$\frac{42-7x}{3}$，根据矩形面积公式列出函数关系式即可；
②将①中函数关系式配方成二次函数的顶点式，可得面积最大时x的值，可得；
③由②可知窗框的最大面积．

解答 解：①根据题意，竖向木料总长为7x米，横向木料总长为42-7x米，
则窗框的高为3x，宽为$\frac{42-7x}{3}$，
∴窗框面积S=3x•$\frac{42-7x}{3}$=-7x²+42x；
②∵S=-7x²+42x=-7（x-3）²+63，
∴当x=3时，S最大，最大值为63m²；
答：当上框架高为3米，下框架的高为6米时，光线通过的窗框面积最大；
③由②可知窗框的最大面积为63m²．

点评 本题主要考查二次函数的应用能力，由题意表示出各部分的长度是解题的前提，根据矩形面积列出函数关系式并配方求最值是解题关键．