
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,四边形ABCD,连接AC,∠ABC=∠BAC=∠DAC=$\frac{1}{2}$∠ADC,若DC=2AD=4,则△ABC的面积为3$\sqrt{15}$.
已知,四边形ABCD,连接AC,∠ABC=∠BAC=∠DAC=$\frac{1}{2}$∠ADC,若DC=2AD=4,则△ABC的面积为3$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
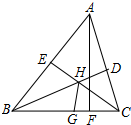 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )| A. | 95 | B. | 65 | C. | 50 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com