
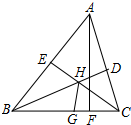
 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①正确,可以根据∠BHC=180°-$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠ACB=180°-$\frac{1}{2}$(180°-∠BAC)解决.
②错误.如果成立,推出∠BAC=60°,显然不可能由此对称结论.
③正确,可以先证明BD⊥AC,再证明△BDA≌△BDC即可.
解答 解:∵BD,CE分别平分∠ABC,∠ACB,
∴∠HBC=$\frac{1}{2}∠$ABC,∠HCG=$\frac{1}{2}∠$ACB,
∵∠BHC=180°-∠HBC-∠HCB,
∴∠BHC=180°-$\frac{1}{2}$∠ABC-$\frac{1}{2}$∠ACB=180°-$\frac{1}{2}$(180°-∠BAC),
∴∠BHC=90°+∠BAC;故①正确;
在△CHG和△CHD中,
$\left\{\begin{array}{l}{CH=CH}\\{∠HCD=∠HCG}\\{CD=CG}\end{array}\right.$,
∴△CHD≌△CHG,
∴∠CHD=∠CHG,
若HG平分∠BHC,则∠BHG=∠CHG=∠CHD=60°,∠BHC=120°,
由①可知∠BAC=60°,显然题目没有这个条件,故②错误.
∵HG∥AF,AF⊥BC,
∴∠HGC=∠AFC=90°,
∵△HCD≌△HCG,
∴∠HDC=∠HGC=90°,
∴BD⊥AC,
在△BDA和△BDC中,
$\left\{\begin{array}{l}{∠ABD=∠CBD}\\{BD=BD}\\{∠BDA=∠BDC}\end{array}\right.$,
∴△BDA≌△BDC,
∴BA=BC,
∴△ABC是等腰三角形,故③正确.
故选C.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、角平分线的定义等知识,解题的关键是寻找全等三角形,利用全等三角形的性质解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
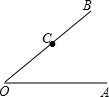 我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.
我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )°.| A. | 64 | B. | 52 | C. | 38 | D. | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
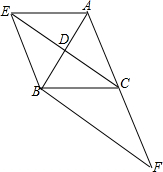 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
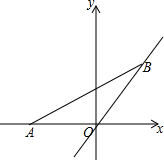 如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).
如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com