
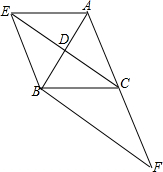
 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.分析 (1)由平行线的性质得出∠AED=∠BCD,由AAS证明△ADE≌△BCD,得出对应边相等AE=BC,即可得出四边形AEBC是平行四边形;
(2)由直角三角形斜边上的中线性质得出BC=$\frac{1}{2}$AF=AC,即可得出结论.
解答 (1)证明:∵在三角形ABC中,CD是中线,
∴AD=BD,
∵AE∥BC,
∴∠AED=∠BCD,
在△ADE和△BCD中,
$\left\{\begin{array}{l}{∠AED=∠BCD}&{\;}\\{∠ADE=∠BDC}&{\;}\\{AD=BD}&{\;}\end{array}\right.$,
∴△ADE≌△BCD(AAS),
∴AE=BC,
又∵AE∥BC,
∴四边形AEBC是平行四边形;
(2)解:△ABF满足∠ABF=90°时,四边形AEBC是菱形;理由如下:
∵∠ABF=90°,CF=AC,
∴BC=$\frac{1}{2}$AF=AC,
∴平行四边形时AEBC是菱形.
故答案为:∠ABF=90°.
点评 本题考查了菱形的判定、平行四边形的判定、平行线的性质、全等三角形的判定与性质;熟练掌握菱形的判定,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
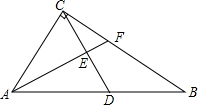 在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.
在Rt△ABC中,∠ACB=90°,AB=5,sin∠CAB=$\frac{4}{5}$,D是斜边AB上一点,过点A作AE⊥CD,垂足为E,AE的延长线交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
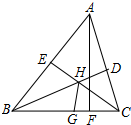 如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.
如图,AF是△ABC的高,角平分线BD、CE交于点H,点G在BC上,CG=CD,下列结论:①∠BHC=90°+∠BAC;②HG平分∠BHC;③若HG∥AF,则△ABC为等腰三角形,其中正确的结论有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.
某县“贡江新区”位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A、B两个工程队先后接力完成,A工程队每天整治12米,B工程队每天整治8米,共用时20天.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
如图,AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )| A. | 95 | B. | 65 | C. | 50 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 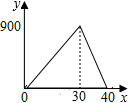 | C. | 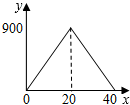 | D. | 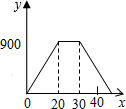 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
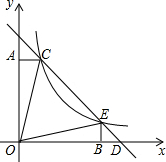 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com