
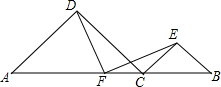
 已知△ADC和△BCE均为等腰直角三角形,F是AB的中点,探究DF与EF的关系.
已知△ADC和△BCE均为等腰直角三角形,F是AB的中点,探究DF与EF的关系. 分析 延长DF到G,使FG=DF,连接DE,EG,GD,证得△AFD≌△BFG,根据全等三角形的性质得到BG=AD,∠GBF=∠A根据等腰直角三角形的性质得到AD=DC,CE=BE,∠A=∠DCA=∠ECB=∠EBC=45°,根据角的和差关系求得∠DCE=∠EBG推出△DCE≌△GBE,根据全等三角形的性质得到DE=EG,如何有等腰三角形的性质即可得到结论.
解答 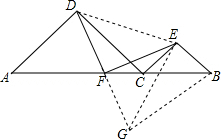 解:延长DF到G,使FG=DF,连接DE,EG,GD,
解:延长DF到G,使FG=DF,连接DE,EG,GD,
∵F是AB的中点,
∴AF=BF,
∵∠DFA=∠EFB,
在△AFD与△BFG中,$\left\{\begin{array}{l}{AF=FG}\\{∠AFD=∠BFG}\\{DF=FG}\end{array}\right.$,
∴△AFD≌△BFG,
∴BG=AD,∠GBF=∠A,
∵△ADC和△BCE均为等腰直角三角形,
∴AD=DC,CE=BE,∠A=∠DCA=∠ECB=∠EBC=45°,
∴∠DCE=180°-∠DCA-∠ECB=180°-45°-45°=90°,∠EBG=∠EBC+∠FBG=∠EBC+∠A=45°+45°=90°,
∴∠DCE=∠EBG,
∴BG=CD,
在△DCE与△GBE中,$\left\{\begin{array}{l}{CD=BG}\\{∠DCE=∠EBG}\\{CE=BE}\end{array}\right.$,
∴△DCE≌△GBE,
∴DE=EG,
∵DF=FG,
∴EF⊥DG,
∴DF⊥EF.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 方程的解是x=m | B. | m>0时,方程的解是正数 | ||
| C. | m<0时,方程的解是正数 | D. | 无论m取何值,方程都不会无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
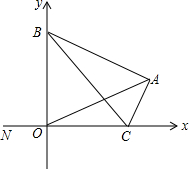 如图所示,在平面直角坐标系xOy中,△ABC的顶点B是y轴正半轴上一个定点,D是BO的中点.点C在x轴上,A在第一象限,且满足AB=AO,N是x轴负半轴上一点,∠BCN=∠BAO=α.
如图所示,在平面直角坐标系xOy中,△ABC的顶点B是y轴正半轴上一个定点,D是BO的中点.点C在x轴上,A在第一象限,且满足AB=AO,N是x轴负半轴上一点,∠BCN=∠BAO=α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明骑自行车从甲地到乙地.如图,折线表示小明途中所花时间t(h)与行程s(km)之间的函数关系.
小明骑自行车从甲地到乙地.如图,折线表示小明途中所花时间t(h)与行程s(km)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com