
【题目】如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).

(1)若△BDE是以BE为底的等腰三角形,求t的值;
(2)若△BDE为直角三角形,求t的值;
(3)当S△BCE≤![]() 时,所有满足条件的t的取值范围 (所有数据请保留准确值,参考数据:tan15°=2﹣
时,所有满足条件的t的取值范围 (所有数据请保留准确值,参考数据:tan15°=2﹣![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() 秒或3秒;(3)6﹣3
秒或3秒;(3)6﹣3![]() ≤t≤3
≤t≤3
【解析】
(1)如图1,先由勾股定理求得AB的长,根据点A、E关于直线CD的对称,得CD垂直平分AE,根据线段垂直平分线的性质得:AD=DE,所以AD=DE=BD,由AB=3![]() ,可得t的值;
,可得t的值;
(2)分两种情况:
①当∠DEB=90°时,如图2,连接AE,根据AB=3t=3![]() ,可得t的值;
,可得t的值;
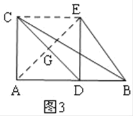
②当∠EDB=90°时,如图3,根据△AGC≌△EGD,得AC=DE,由AC∥ED,得四边形CAED是平行四边形,所以AD=CE=3,即t=3;
(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE面积的变化取决于以CE作底边时,对应高的大小变化,
①当△BCE在BC的下方时,
②当△BCE在BC的上方时,
分别计算当高为3时对应的t的值即可得结论.
解:(1)如图1,连接AE,
由题意得:AD=t,
∵∠CAB=90°,∠CBA=30°,
∴BC=2AC=6,
∴AB=![]() =3
=3![]() ,
,
∵点A、E关于直线CD的对称,
∴CD垂直平分AE,
∴AD=DE,
∵△BDE是以BE为底的等腰三角形,
∴DE=BD,
∴AD=BD,
∴t=AD=![]() ;
;
(2)△BDE为直角三角形时,分两种情况:
①当∠DEB=90°时,如图2,连接AE,
∵CD垂直平分AE,
∴AD=DE=t,
∵∠B=30°,
∴BD=2DE=2t,
∴AB=3t=3![]() ,
,
∴t=![]() ;
;
②当∠EDB=90°时,如图3,
连接CE,
∵CD垂直平分AE,
∴CE=CA=3,
∵∠CAD=∠EDB=90°,
∴AC∥ED,
∴∠CAG=∠GED,
∵AG=EG,∠CGA=∠EGD,
∴△AGC≌△EGD,
∴AC=DE,
∵AC∥ED,
∴四边形CAED是平行四边形,
∴AD=CE=3,即t=3;
综上所述,△BDE为直角三角形时,t的值为![]() 秒或3秒;
秒或3秒;
(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE面积的变化取决于以CE作底边时,对应高的大小变化,
①当△BCE在BC的下方时,过B作BH⊥CE,交CE的延长线于H,如图4,当AC=BH=3时,
此时S△BCE=![]() AEBH=
AEBH=![]() ×3×3=
×3×3=![]() ,
,
易得△ACG≌△HBG,
∴CG=BG,
∴∠ABC=∠BCG=30°,
∴∠ACE=60°﹣30°=30°,
∵AC=CE,AD=DE,DC=DC,
∴△ACD≌△ECD,
∴∠ACD=∠DCE=15°,
tan∠ACD=tan15°=![]() =2﹣
=2﹣![]() ,
,
∴t=6﹣3![]() ,
,
由图形可知:0<t<6﹣3![]() 时,△BCE的BH越来越小,则面积越来越小,
时,△BCE的BH越来越小,则面积越来越小,
②当△BCE在BC的上方时,如图3,CE=ED=3,且CE⊥ED,
此时S△BCE=![]() CEDE=
CEDE=![]() ×3×3=
×3×3=![]() ,此时t=3,
,此时t=3,
综上所述,当S△BCE≤![]() 时,t的取值范围是6﹣3
时,t的取值范围是6﹣3![]() ≤t≤3.
≤t≤3.





 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
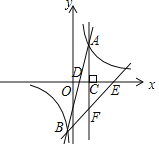
【题目】如图,一次函数y=kx+b和反比例函数![]() 的图象相交于A(2,4)、B(﹣1,n)两点,一次函数的图象交x轴于点D.
的图象相交于A(2,4)、B(﹣1,n)两点,一次函数的图象交x轴于点D.
(1)直接写出一次函数与反比例函数的解析式.
(2)请结合函数图象,直接写出不等式![]() 的解集.
的解集.
(3)过点A作直线AC⊥x轴,垂足为点C,过点B的直线交x轴于点E,交直线AC于点F,若△ECF∽△ACD,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.

请你结合这些算式,解答下列问题:
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n–1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
A. 甲队每天修路20米
B. 乙队第一天修路15米
C. 乙队技术改进后每天修路35米
D. 前七天甲,乙两队修路长度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
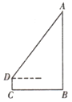
【题目】如图,小明为了测量校园里旗杆![]() 的高度,将测角仪
的高度,将测角仪![]() 竖直放在距旗杆底部
竖直放在距旗杆底部![]() 点
点![]() 的位置,在
的位置,在![]() 处测得旗杆顶端
处测得旗杆顶端![]() 的仰角为
的仰角为![]() ,若测角仪的高度是
,若测角仪的高度是![]() ,则旗杆
,则旗杆![]() 的高度约为(精确到
的高度约为(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )( )
)( )
A. 8.5米B. 9米C. 9.5米D. 10米
查看答案和解析>>
科目:初中数学 来源: 题型:
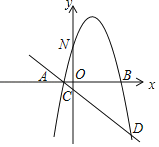
【题目】如图,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:
与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:![]() 与y轴交于点C,与抛物线
与y轴交于点C,与抛物线![]() 的另一个交点为D,已知
的另一个交点为D,已知![]() ,P点为抛物线
,P点为抛物线![]() 上一动点(不与A、D重合).
上一动点(不与A、D重合).
(1)求抛物线和直线l的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作![]() 轴交直线l于点F,求
轴交直线l于点F,求![]() 的最大值;
的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
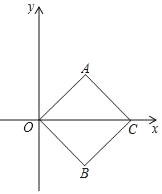
【题目】如图,四边形AOBC是正方形,点C的坐标是(4![]() ,0).
,0).
(Ⅰ)正方形AOBC的边长为 ,点A的坐标是 .
(Ⅱ)将正方形AOBC绕点O顺时针旋转45°,点A,B,C旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(Ⅲ)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时同时停止运动,当△OPQ为等腰三角形时,求出t的值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有5000只鸡准备对外出售。从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图①和图②。请根据相关信息,解答下列问题:
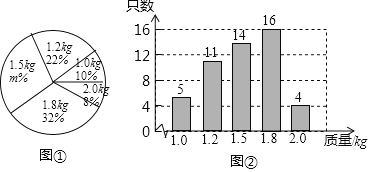
Ⅰ.图①中![]() 的值为 ;
的值为 ;
Ⅱ.求统计的这组数据的平均数、众数和中位数;
Ⅲ.根据样本数据,估计这5000只鸡中,质量为1.0kg的约为多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com