
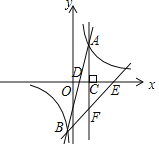
【题目】如图,一次函数y=kx+b和反比例函数![]() 的图象相交于A(2,4)、B(﹣1,n)两点,一次函数的图象交x轴于点D.
的图象相交于A(2,4)、B(﹣1,n)两点,一次函数的图象交x轴于点D.
(1)直接写出一次函数与反比例函数的解析式.
(2)请结合函数图象,直接写出不等式![]() 的解集.
的解集.
(3)过点A作直线AC⊥x轴,垂足为点C,过点B的直线交x轴于点E,交直线AC于点F,若△ECF∽△ACD,求点E的坐标.
【答案】(1)y![]() 、y=4x﹣4;(2)x<﹣1或0<x<2;(3)点E坐标为(31,0)或(﹣33,0).
、y=4x﹣4;(2)x<﹣1或0<x<2;(3)点E坐标为(31,0)或(﹣33,0).
【解析】
(1)把点A坐标代入![]() 可求出m的值,即可得出反比例函数的解析式,并B(-1,n)代入反比例函数解析式可得n的值,即可得出B点坐标,把A、B两点坐标代入y=kx+b可求出k、b的值,即可得一次函数解析式;(2)根据A、B坐标,结合图象即可得出不等式
可求出m的值,即可得出反比例函数的解析式,并B(-1,n)代入反比例函数解析式可得n的值,即可得出B点坐标,把A、B两点坐标代入y=kx+b可求出k、b的值,即可得一次函数解析式;(2)根据A、B坐标,结合图象即可得出不等式![]() 的解集;(3)过点B作BM⊥x轴于点M,根据一次函数的解析式可求出D点坐标,根据A、B、D三点坐标可得AC=4,OC=2,OM=1,BM=8,OD=1,CD=1,由AC⊥x轴,BM⊥x轴可得△ECF∽△EMB,即可证明△ACD∽△EMB,根据相似三角形的性质可求出EM的长,即可求出OE的长,进而可得E点坐标.
的解集;(3)过点B作BM⊥x轴于点M,根据一次函数的解析式可求出D点坐标,根据A、B、D三点坐标可得AC=4,OC=2,OM=1,BM=8,OD=1,CD=1,由AC⊥x轴,BM⊥x轴可得△ECF∽△EMB,即可证明△ACD∽△EMB,根据相似三角形的性质可求出EM的长,即可求出OE的长,进而可得E点坐标.
(1)把点A(2,4)代入反比例函数![]() 表达式得:m=8,
表达式得:m=8,
∴反比例函数的解析式为:y![]() ,
,
∵点B(-1,n)在反比例函数上,
∴n=![]() =-8.
=-8.
∴点B(﹣1,﹣8),
将点A、B的坐标代入一次函数表达式得:![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为:y=4x﹣4.
(2)∵A(2,4),B(-1,-8)
∴由图象可以看出不等式![]() 的解集为:x<﹣1或0<x<2;
的解集为:x<﹣1或0<x<2;
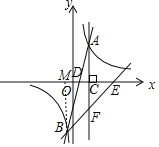
(3)过点B作BM⊥x轴于点M,
∵点A(2,4)、B(-1,-8)
∴AC=4,OC=2,OM=1,BM=8,
∵y=4x﹣4与x轴交于点D,
∴当y=0时,x=1,即D(1,0)
∴OD=1,CD=1,
∵AC⊥x轴,BM⊥x轴,
∴△ECF∽△EMB,
∵△ECF∽△ACD,
∴△ACD∽△EMB,
∴![]() ,即:
,即:![]() ,
,
∴EM=32,
∴OE=31或33,
点E坐标为(31,0)或(﹣33,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
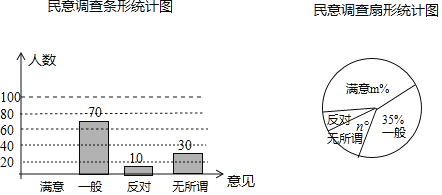
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
(1)将△ABC向左平移3个单位,再向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
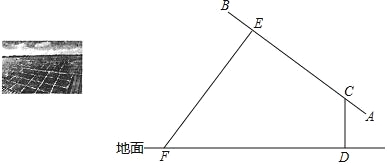
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
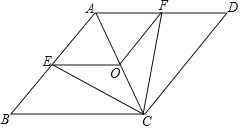
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
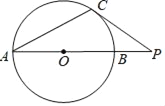
【题目】如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线.
(2)求tan∠CAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种小商品,每件进货价为190元.调查发现,当销售价为210元时,平均每天能销售8件;当销售价每降低2元时,平均每天就能多销售4件.设每件小商品降价![]() 元,平均每天销售
元,平均每天销售![]() 件.
件.
(1)直接写出![]() 与
与![]() 之间的函数关系式(不必写出
之间的函数关系式(不必写出![]() 的取值范围);
的取值范围);
(2)商场要想使这种小商品平均每天的销售利润达到280元,求每件小商品的销售价应定为多少元?
(3)设每天的销售总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;每件商品降价多少元时,每天的总利润最大?最大利润是多少?
之间的函数关系式;每件商品降价多少元时,每天的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).

(1)若△BDE是以BE为底的等腰三角形,求t的值;
(2)若△BDE为直角三角形,求t的值;
(3)当S△BCE≤![]() 时,所有满足条件的t的取值范围 (所有数据请保留准确值,参考数据:tan15°=2﹣
时,所有满足条件的t的取值范围 (所有数据请保留准确值,参考数据:tan15°=2﹣![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com