
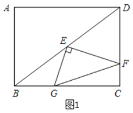
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是对角线BD的中点,直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G.
(1)若点F是边CD的中点,求EG的长;
(2)当直角∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC交于点F、G.∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值;
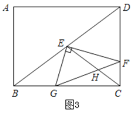
(3)如图3,连接CE交FG于点H,若![]() ,请求出CF的长.
,请求出CF的长.

【答案】(1)3;(2)∠EFG的大小不发生变化,理由见详解;![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据点E是对角线BD的中点,点F是边CD的中点,可证![]() ,再根据
,再根据![]() 可得四边形EGCF是矩形,则点G是边BC的中点,可求出EG;
可得四边形EGCF是矩形,则点G是边BC的中点,可求出EG;
(2)作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,可得
,可得![]() 是
是![]() 绕直角顶点E旋转而得到的,利用
绕直角顶点E旋转而得到的,利用![]() ,
,![]() ,易证
,易证![]() ,根据相似比
,根据相似比![]() 可得
可得![]() ,则有
,则有![]() ,可知
,可知![]() 的大小在转动的过程中不会发生变化;利用
的大小在转动的过程中不会发生变化;利用![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,则
,则![]() ;
;
(3)连接CE交FG于点H,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,过点E作
,过点E作![]() 交
交![]() 于
于![]() ,则
,则![]() 是
是![]() 绕直角顶点E旋转而得到的,由(2)知
绕直角顶点E旋转而得到的,由(2)知![]() 的大小在转动的过程中不会发生变化,易证
的大小在转动的过程中不会发生变化,易证![]() ,则
,则![]() ,有
,有![]() ,可得
,可得![]() ,设
,设![]() ,则
,则![]() ,可求得
,可求得![]() ,
,![]() ,利用勾股定理即可求出
,利用勾股定理即可求出![]() 的值,即可得到
的值,即可得到![]() 的值.
的值.
解:(1)如图示,

∵点E是对角线BD的中点,点F是边CD的中点,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴四边形EGCF是矩形,
∴![]() ,
,
∴点G是边BC的中点,
∴![]() ;
;
(2)答:∠EFG的大小不会发生变化。
证明:如图示:作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]()
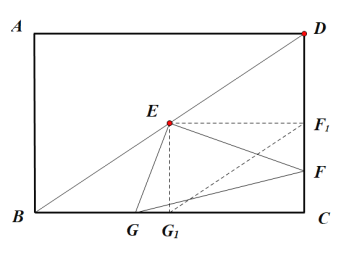
∴![]() ,
,![]() ,
,
∴![]() 是
是![]() 绕直角顶点E旋转而得到的,
绕直角顶点E旋转而得到的,
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 的大小在转动的过程中不会发生变化;
的大小在转动的过程中不会发生变化;
∵点E是对角线BD的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]()
(3)如图示,连接CE交FG于点H,作![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,过点E作
,过点E作![]() 交
交![]() 于
于![]() ,
,
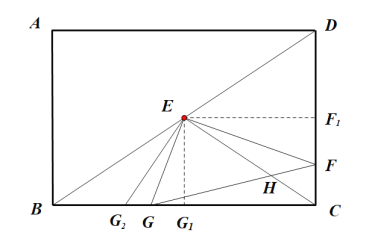
则![]() 是
是![]() 绕直角顶点E旋转而得到的,
绕直角顶点E旋转而得到的,
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即:
,即:![]() ,
,
设![]() ,则
,则![]() ,
,
由(2)可知:![]() ,
,![]() ,
,![]()
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,解之得:
,解之得:![]() (取正值),
(取正值),
即:![]() .
.


科目:初中数学 来源: 题型:
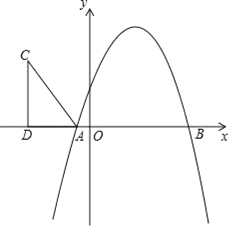
【题目】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DE=DF;②∠CME=∠CDE;③DG2=GN GE;④若BF=2,![]() 则正确的结论有( )个.
则正确的结论有( )个.
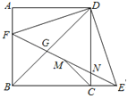
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
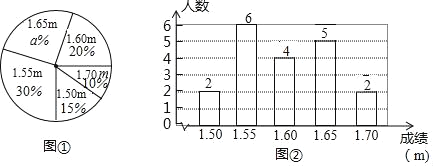
(Ⅰ)图①中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(Ⅲ)根据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABE中,∠B=90°,AB=BE,将△ABE绕点A逆时针旋转45°,得到△AHD,过D作DC⊥BE交BE的延长线于点C,连接BH并延长交DC于点F,连接DE交BF于点O.下列结论:①DE平分∠HDC;②DO=OE;③H是BF的中点;④BC-CF=2CE;⑤CD=HF,其中正确的有( )
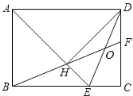
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:

说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀);等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整):
c.乙企业样本数据的频数分布直方图如下:

d.两企业样本数据的平均数、中位数、众数、极差、方差如下:

根据以上信息,回答下列问题:
(1)![]() 的值为__________,
的值为__________,![]() 的值为______________;
的值为______________;
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为_____________;
若乙企业生产的某批产品共5万件,估计质量优秀的有_____________万件;
(3)根据图表数据,你认为___________企业生产的产品质量较好,理由为:__________________.(至少从两个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
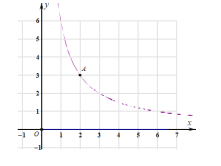
【题目】如图,在平面直角坐标系 xOy中,反比例函数 y ![]() x 0 的图象经过点 A2,3 ,直线y ax , y
x 0 的图象经过点 A2,3 ,直线y ax , y ![]() 与反比例函数 y
与反比例函数 y ![]() x 0 分别交于点 B,C两点.
x 0 分别交于点 B,C两点.
(1)直接写出 k 的值 ;
(2)由线段 OB,OC和函数 y ![]() x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
① 当 A点与 B点重合时,直接写出区域 W 内的整点个数 ;
② 若区域 W内恰有 8个整点,结合函数图象,直接写出 a的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com