
分析 (1)首先证明△BEC≌△ADC,由∠EBC=∠DAC,∠BDF=∠CDA,可证得∠BFD=∠DCA=90°;
(2)当0≤x≤4$\sqrt{2}$时,S=S△ABC-S△BFH-S△GCC′-S△AKC′;当4$\sqrt{2}$<x<10时,S=平行四边形E′C′AH的面积-△AKC′的面积;
(3)首先根据题意画出图形,然后由等腰三角形的性质即可求得答案.
解答 解:(1)AF⊥BE.
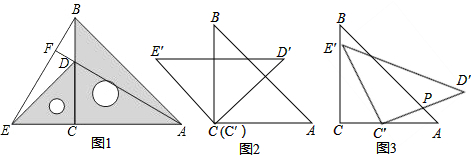
∵△EDC和△ABC均为等腰直角三角形,
∴∠ECD=∠BCA,DC=EC,CB=CA.
在△BEC和△ADC中,$\left\{\begin{array}{l}{DC=EC}\\{∠ECD=∠BCA}\\{CB=CA}\end{array}\right.$,
∴△BEC≌△ADC.
∴∠EBC=∠DAC.
又因为∠BDF=∠CDA,
∴∠BFD=∠DCA=90°.
∴AF⊥BE.
(2)如图2所示: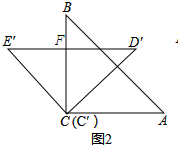
∵∠BCD′=45°,
∴∠E′CF=∠FE′C=45°.
∴FC2+E′F2=E′C2,即2FC2=82.
∴FC=4$\sqrt{2}$.
∴BF=10-4$\sqrt{2}$
如图4所示:设CC′=x,则C′A=10-x.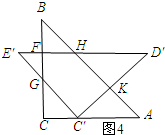
S=S△ABC-S△BFH-S△GCC′-S△AKC′
=$\frac{1}{2}×10×10$-$\frac{1}{2}×(10-4\sqrt{2})^{2}$-$\frac{1}{2}{x}^{2}$-$\frac{1}{2}×\frac{1}{2}(10-x)^{2}$.
整理得:S=$-\frac{3}{4}{x}^{2}+5x+40\sqrt{2}-41$(0≤x≤4$\sqrt{2}$);
如图5所示: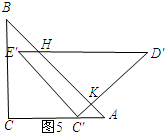
S=平行四边形E′C′AH的面积-△AKC′的面积=$4\sqrt{2}×(10-x)$-$\frac{1}{2}×\frac{1}{2}(10-x)^{2}$.
整理得:S=$-\frac{1}{4}{x}^{2}+(5-4\sqrt{2})x+40\sqrt{2}-25$(4$\sqrt{2}$<x<10).
综上所述,当0≤x≤4$\sqrt{2}$时,S=$-\frac{3}{4}{x}^{2}+5x+40\sqrt{2}-41$;当4$\sqrt{2}$<x<10时,S=$-\frac{1}{4}{x}^{2}+(5-4\sqrt{2})x+40\sqrt{2}-25$.
(3)如图6所示: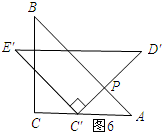
当∠PC′A=∠A=45°时,△APC′为等腰三角形.此时a=0.
如图7所示: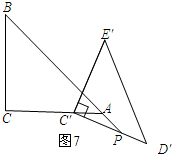
当∠AC′P=∠APC′时,△APC′为等腰三角形,
由三角形的外角的性质可知:∠AC′P+∠APC′=∠BAC=45°,
又∵∠AC′P=∠APC′
∴∠AC′P=$\frac{1}{2}∠BAC$=$\frac{1}{2}×45°$=22.5°.
∴a=45°+22.5°=67.5°.
点评 本题主要考查的是全等三角形的性质和判定、等腰三角形的性质、列函数关系式,根据题意画出符合题意的图形,能够将不规则图形的面积转为规则图形的面积是解题的关键.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
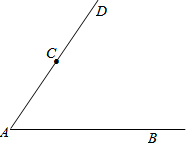 尺规作图(在原图上作图,不写作法,保留作图痕迹)在下列图形中,补充作图:
尺规作图(在原图上作图,不写作法,保留作图痕迹)在下列图形中,补充作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com