
【题目】已知在平面直角坐标系中,点O是坐标原点,A(﹣2,2),过A作AB⊥y轴于点B,以OB为边在第一象限内作△BCO.

(1)如图①,若△BCO为等边三角形,求点C坐标;
(2)如图②,若△BCO为以BO为斜边的直角三角形,求AC的最大值;
(3)如图③,若∠BCO=45°,BC=a,CO=b,请用a、b的代数式表示AC的长.
【答案】(1)点 C(![]() ,1);(2)AC的最大值为
,1);(2)AC的最大值为![]() +1;(3)AC=
+1;(3)AC=![]() .
.
【解析】
(1)过点C作CE⊥OB于点E,由等边三角形的性质可求BC=BO=CO=2,BE=EO=1,由勾股定理可求CE的长,即可求点C坐标;
(2)取BO中点E,连接AE,由勾股定理可求AE的长,由点C在以E为圆心,OE长为半径的圆上,即当点C在线段AC的延长线上时,AC有最大值,则可求AC的最大值;
(3)过点B作BF⊥OC于点F,过点C作CE⊥OB于点 E,CH⊥AB于H,由直角三角形的性质可求BF=CF=![]() BC=
BC=![]() a,由面积法可求CE的长,由勾股定理可求BE2,AC的值.
a,由面积法可求CE的长,由勾股定理可求BE2,AC的值.
解:(1)如图1,过点C作CE⊥OB于点E,
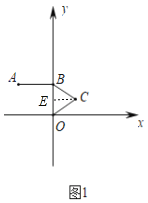
∵A(﹣2,2),过A作AB⊥y轴于点B,
∴点B(0,2),
∵△BCO是等边三角形,CE⊥BO,
∴BC=BO=CO=2,BE=EO=1,
∴CE=![]() ,
,
∴点 C(![]() ,1);
,1);
(2)如图2,取BO中点E,连接AE,
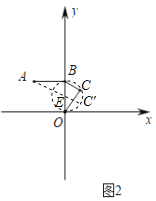
∵点E是BO中点,
∴OE=BE=1,
∴AE=![]() ,
,
∵△BCO为以BO为斜边的直角三角形,
∴点C在以E为圆心,OE长为半径的圆上,
∴当点C在线段AC的延长线上时,AC有最大值,
即AC的最大值为![]() +1;
+1;
(3)如图3,过点B作BF⊥OC于点F,过点C作CE⊥OB于点 E,CH⊥AB于H,
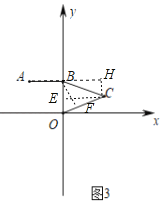
∵BF⊥OC,∠BCO=45°,
∴BF=CF=![]() BC=
BC=![]() a,
a,
∵S△OBC=![]() ×OB×EC=
×OB×EC=![]() ×OC×BF,
×OC×BF,
∴2EC=![]() ba,
ba,
∴EC=![]() ab,
ab,
∴BE2=BC2﹣EC2=a2﹣(![]() ab)2,
ab)2,
∵CH⊥AH,EC⊥OB,OB⊥BH,
∴四边形BHCE是矩形,
∴CH=BE,BH=EC,
∴AC2=AH2+CH2=(2+![]() ab)2+a2﹣(
ab)2+a2﹣(![]() ab)2=a2+
ab)2=a2+![]() ab+4
ab+4
∴AC=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 135° B. 130° C. 125°
D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
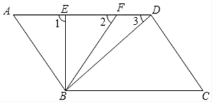
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,已知A(2,2)、B(﹣2,0)、C(﹣1,﹣2).

(1)在平面直角坐标系中画出△ABC;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)求△ABC的面积;
(4)已知点P为x轴上一点,若S△ABP=5时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数。

①若∠ABC=40°,∠ACB=60°,则∠BIC=______°;
②若∠ABC+∠ACB=100°,则∠BIC=___________°;
③若∠A=80°,则∠BIC=_______°;
④从上述计算中,我们能发现已知∠A=x,则∠BIC=_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴上;∠COA=∠B=60°,且CB∥OA.
(1)求证,四边形OABC是平行四边形.
(2)若A的坐标为(8,0),OC长为6,求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.

(1)求证:CD∥A′B;
(2)若AB=4,求A′B2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com