
【题目】如图,ΔABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数。

①若∠ABC=40°,∠ACB=60°,则∠BIC=______°;
②若∠ABC+∠ACB=100°,则∠BIC=___________°;
③若∠A=80°,则∠BIC=_______°;
④从上述计算中,我们能发现已知∠A=x,则∠BIC=_______°.
【答案】①130;②130;③130;④90°+![]() .
.
【解析】
①由∠ABC=40°,∠ACB=60°,∠ABC与∠ACB的平分线交于点I,可求∠IBC、∠ICB的度数,再利用三角形内角和定理求∠BIC;
②由∠ABC+∠ACB=100°,∠ABC与∠ACB的平分线交于点I,可求∠IBC+∠ICB的度数,再利用三角形内角和定理求∠BIC;
③由∠A=80°可得∠ABC+∠ACB=100°,∠ABC与∠ACB的平分线交于点I,可求∠IBC+∠ICB的度数,再利用三角形内角和定理求∠BIC;
④由三角形内角和定理得∠ABC+∠ACB=180°﹣∠A,∠ABC与∠ACB的平分线交于点I,则∠IBC+∠ICB![]() (180°﹣∠A).在△IBC中,利用三角形内角和定理求∠BIC.
(180°﹣∠A).在△IBC中,利用三角形内角和定理求∠BIC.
①∵∠ABC=40°,∠ACB=60°,∠ABC与∠ACB的平分线交于点I,∴∠IBC=20°∠ICB=30°,∴∠BIC=180°﹣∠IBC﹣∠ICB=130°;
②∵∠ABC+∠ACB=100°,∠ABC与∠ACB的平分线交于点I,∴∠IBC+∠ICB![]() (∠ABC+∠ACB)=50°,∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
(∠ABC+∠ACB)=50°,∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
③∵∠A=80°,∴∠ABC+∠ACB=100°.
又∵∠ABC与∠ACB的平分线交于点I,∴∠IBC+∠ICB![]() (∠ABC+∠ACB)=50°,∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
(∠ABC+∠ACB)=50°,∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
④∠BIC=90°![]() x.理由如下:
x.理由如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A.
∵BI、CI是△ABC内角的平分线,∴∠IBC![]() ∠ABC,∠ICB
∠ABC,∠ICB![]() ∠ACB,∴∠IBC+∠ICB
∠ACB,∴∠IBC+∠ICB![]() ∠ABC
∠ABC![]() ∠ACB
∠ACB![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)![]() (180°﹣∠A).
(180°﹣∠A).
在△IBC中,∠BIC=180°﹣(∠IBC+∠ICB)=180°![]() (180°﹣∠A)=90°
(180°﹣∠A)=90°![]() ∠A.
∠A.
即:∠BIC=90°![]() x.
x.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个公共汽车站相向发车,一人在街上行走,他发现每隔8分钟就迎面开来一辆公交车,每隔24分种从背后开来一辆公交车,如果车站发车的间隔时间相同,各车的速度相同,那两车站发车的间隔时间为( )
A. 18分钟 B. 10分钟 C. 12分钟 D. 16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知过点B(1,0)的直线l1:y=kx+b与直线l2:y=2x+4相交于点P(a,2).
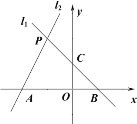
(1) 求直线l1的解析式;
(2) 根据图象直接写出不等式![]() 的解集;
的解集;
(3) 求四边形PAOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D、E 分别在 BC、AC 上且 BD=CE,AD=DE, ∠C =∠ADE, 则∠B =∠C,试填写说理过程.

解因为∠EDB =∠C+∠DEC( )
即∠ADB+∠ADE =∠C+∠DEC
因为∠C =∠ADE( )
所以∠ =∠ (等式性质)
在△ABD 与△DCE 中,

所以△ABD ≌ △DCE( )
所以∠B =∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点O是坐标原点,A(﹣2,2),过A作AB⊥y轴于点B,以OB为边在第一象限内作△BCO.

(1)如图①,若△BCO为等边三角形,求点C坐标;
(2)如图②,若△BCO为以BO为斜边的直角三角形,求AC的最大值;
(3)如图③,若∠BCO=45°,BC=a,CO=b,请用a、b的代数式表示AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三台县某中学“五![]() 四”青年节举行了“班班有歌声”歌咏比赛活动
四”青年节举行了“班班有歌声”歌咏比赛活动![]() 比赛聘请了10位教师和10位学生担任评委,其中甲班的得分情况如统计表和统计图.
比赛聘请了10位教师和10位学生担任评委,其中甲班的得分情况如统计表和统计图.
老师评委评分统计表:
评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
学生评委评分折线统计图师生评委评分频数分布直方图

![]() 补全频数分布直方图.
补全频数分布直方图.
![]() 学生评委评分的中位数是______.
学生评委评分的中位数是______.
![]() 计分办法规定:老师评委、学生评委的评分各去掉一个最高分、一个最低分,并且按教师、学生各占
计分办法规定:老师评委、学生评委的评分各去掉一个最高分、一个最低分,并且按教师、学生各占![]() 、
、![]() 的方法计算各班最后得分,知甲班最后得分
的方法计算各班最后得分,知甲班最后得分![]() 分,试求统计表中的x.
分,试求统计表中的x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)若∠BAC=40°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)求证:EF2+BF2=2AC2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成证明及理由

已知:∠1=∠E,∠B=∠D
求证:AB∥CD
证明:∵ ∠1=∠E( )
∴_______∥_______ ( )
∴ ∠D+∠2=180°( )
∵ ∠B=∠D( )
∴ ∠_______+ ∠_______ = 180°( )
∴ AB∥CD( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com