
 如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为 |
| AC |
 |
| PA |
 |
| AB |
 |
| BG |
 |
| PA |
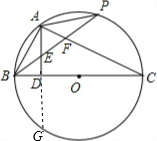 解:(1)AE=BE;
解:(1)AE=BE; |
| AB |
 |
| BG |
 |
| PA |
 |
| AB |
 |
| BG |
 |
| PA |
| AP |
| BC |
| AF |
| BF |
| PF |
| CF |
 |
| AC |


科目:初中数学 来源: 题型:
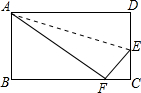 折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
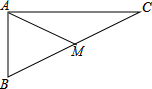 如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.查看答案和解析>>
科目:初中数学 来源: 题型:
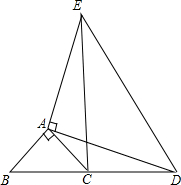 如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.
如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com