
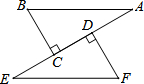
 如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:科目:初中数学 来源: 题型:解答题
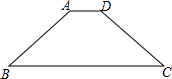 已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.
已知等腰梯形ABCD中,AD=3cm,BC=11cm,腰AB=5cm,点A为圆心,AD为半径的⊙A与底BC有怎样的位置关系?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
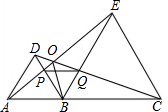 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 停靠站 | 起点站 | 中间 第1站 | 中间 第2站 | 中间 第3站 | 中间 第4站 | 中间 第5站 | 中间 第6站 | 终点站 |
| 上下车人数 | +21 | -3 +8 | -4 +2 | 0 +4 | -7 +1 | -9 +6 | -7 0 | -12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com