
����Ŀ��������̽��.�������ϵ�����һ��P��
��������Nʹ��N��P��ʾ������Ϊ�෴�����ٰ�N��Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P�������dz�P����P��N�任�㣻
�ڰ�P������ƽ��1����λ���õ���M��������P���ʹ��P�����M��ʾ������Ϊ�෴�������dz�P�����P��M�任�㣮
��1����ͼ������P��ʾ�����ǣ�4����P��N�任��P����ʾ������ ________ ��

��2����P��M�任��P�����ʾ������2�����P��ʾ������ ________ ��
��3����P����P����ֱ�ΪP��N�任���M�任�㣬��OP����2OP��������P��ʾ������
���𰸡���1��5����2��-3����3��![]() ��
��![]() ��
��
��������
��1�����ݢٵIJ�������ɵó�P����ʾ������
��2�����P��ʾ����Ϊx�����ݢڵIJ���������-��x+1��=2���ó���P��ʾ������
��3�����P��ʾ����Ϊy����P����ʾ������-y+1��P�����ʾ������-��y+1��������OP����2OP����з��̽�����ɵó���P��ʾ������
�⣺��1���ɢٵã�����P��ʾ������-4�����P����ʾ������-��-4��+1=5��
��2�����P��ʾ����Ϊx�����ݢڵIJ���������-��x+1��=2��
��ã�x=-3��
���P��ʾ������-3��
��3�����P��ʾ����Ϊy����P����ʾ������-y+1��P�����ʾ������-��y+1����
��OP����2OP�����
��![]()
��ã�![]() ��
��![]() ��
��
���P��ʾ������![]() ��
��![]() ��
��
�ʴ�Ϊ����1��5����2��-3����3��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ�����O��BC��ֱ������O������PA��CB���ӳ����ڵ�P��OE��AC��AB�ڵ�F����PA�ڵ�E������BE��
��1���ж�BE����O��λ�ù�ϵ��˵��������
��2������O�İ뾶Ϊ4��BE=3����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �У�AD��BC��CE��AB������ֱ�Ϊ D��E��AD��CE ���ڵ� F���� EF=EB=5�� AE=7���� CF �ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1����ABC�Ķ��㶼�ڷ���ֽ�ĸ���ϣ�����ABC����һ��ƽ�ƺ�õ���A'B'C'��ͼ�б���˵�C�Ķ�Ӧ��C'��
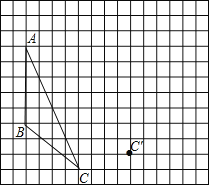
��1���뻭��ƽ�ƺ����A'B'C'��
��2��������AA'��BB'�����������߶εĹ�ϵ�� ��
��3������������ABC��AC���ϵ�����BD�Լ�AB���ϵĸ�CE��
��4���߶�AB��ƽ�ƹ�����ɨ����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=90����AC=12��BC=9��AB=15��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��3����λ�����˶���ʱ��Ϊt�룮
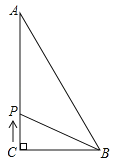
��1����t=�� ��ʱ��CP����ABC������ֳ���ȵ������֣�
��2����t=5ʱ��CP����ABC�ֳɵ����������֮����![]() =�� ��.
=�� ��.
��3������BPC�����Ϊ18������t��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2+��2m+1��x + m2��1��x�ύ��A��B������ͬ�ĵ㣮
��1����m��ȡֵ��Χ��
��2��д��һ������������m��ֵ�������ʱA��B��������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������ABC�ĵ�Ϊ30������BCΪֱ���ġ�O��ױ�AB���ڵ�D����D��DE��AC������ΪE��
��1��֤����DEΪ��O�����ߣ�
��2������OE����BC=4������OEC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���A��t��1��1�����B���ڹ��㣨t��0���Ҵ�ֱ��x���ֱ�߶Գƣ�
��1����ABΪ�ױ�������������ABC��
�ٵ�t��2ʱ����B������Ϊ�� ����
�ڵ�t��0.5��ֱ��AC����ԭ��Oʱ����C��x��ľ���Ϊ�� ����
����![]() �����е㵽y��ľ��붼��С��1����t��ȡֵ��Χ���� ����
�����е㵽y��ľ��붼��С��1����t��ȡֵ��Χ���� ����
��2����ABΪб��������ֱ��������ABD��ֱ��m���㣨0��b������x��ƽ�У���ֱ��m�ϴ��ڵ�P��![]() �ϴ��ڵ�K������PK��1��ֱ��д��b��ȡֵ��Χ��
�ϴ��ڵ�K������PK��1��ֱ��д��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������800��A������A�����һ��¥��C�ĸ�����30�㣬����������ˮƽ������˴�¥����400��ﵽB������B���ٴβ�ô˴�¥¥��C�ĸ�����45�㣬��ô�¥CD�ĸ߶ȣ�
�ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
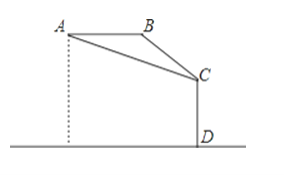
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com