
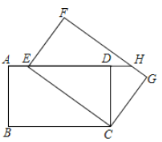
【题目】如图,将矩形ABCD绕点C旋转得到矩形EFGC,点E在AD上.延长AD交FG于点H
(1)求证:△EDC≌△HFE;
(2)若∠BCE=60°,连接BE、CH.证明:四边形BEHC是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)依据题意可得到FE=AB=DC,∠F=∠EDC=90°,FH∥EC,利用平行线的性质可证明∠FHE=∠CED,然后依据AAS证明△EDC≌△HFE即可;
(2)首先证明四边形BEHC为平行四边形,再证明邻边BE=BC即可证明四边形BEHC是菱形.
(1)证明:∵矩形FECG由矩形ABCD旋转得到,
∴FE=AB=DC,∠F=∠EDC=90°,FH∥EC,
∴∠FHE=∠CED.
在△EDC和△HFE中,
 ,
,
∴△EDC≌△HFE(AAS);
(2)∵△EDC≌△HFE,
∴EH=EC.
∵矩形FECG由矩形ABCD旋转得到,
∴EH=EC=BC,EH∥BC,
∴四边形BEHC为平行四边形.
∵∠BCE=60°,EC=BC,
∴△BCE是等边三角形,
∴BE=BC,
∴四边形BEHC是菱形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.

(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
(1)求证:△ABD∽△DCE;
(2)若CD=12,CE=3,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:形如y=|G|(G为用自变量表示的代数式)的函数叫做绝对值函数.
例如,函数y=|x﹣1|,y=![]() ,y=|﹣x2+2x+3|都是绝对值函数.
,y=|﹣x2+2x+3|都是绝对值函数.
绝对值函数本质是分段函数,例如,可以将y=|x|写成分段函数的形式:![]() .
.
探索并解决下列问题:
(1)将函数y=|x﹣1|写成分段函数的形式;
(2)如图1,函数y=|x﹣1|的图象与x轴交于点A(1,0),与函数y=![]() 的图象交于B,C两点,过点B作x轴的平行线分别交函数y=
的图象交于B,C两点,过点B作x轴的平行线分别交函数y=![]() ,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
(3)已知函数y=|﹣x2+2x+3|的图象与y轴交于F点,与x轴交于M,N两点(点M在点N的左边),点P在函数y=|﹣x2+2x+3|的图象上(点P与点F不重合),PH⊥x轴,垂足为H.若△PMH与△MOF相似,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区规划在一个长50米,宽30米的矩形场地ABCD上,修建三条同样宽的道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪面积都为178平方米,设道路宽度为x米,则( )

A.(50﹣2x)(30﹣x)=178×6
B.30×50﹣2×30x﹣50x=178×6
C.(30﹣2x)(50﹣x)=178
D.(50﹣2x)(30﹣x)=178
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
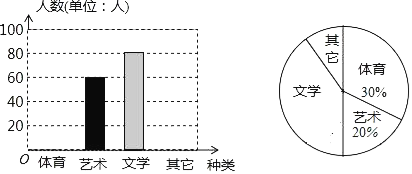
(1)此次共调查了多少人?
(2)求体育社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有3000名学生,请估计喜欢文学类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com