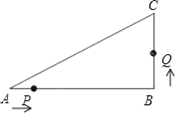
【题目】如图，已知在△ABC中，∠B=90°，AB=8cm，BC=6cm，点P开始从点A开始沿△ABC的边做逆时针运动，且速度为每秒1cm，点Q从点B开始沿△ABC的边做逆时针运动，且速度为每秒2cm，他们同时出发，设运动时间为t秒．
（1）出发2秒后，求PQ的长；
（2）在运动过程中，△PQB能形成等腰三角形吗？若能，则求出几秒后第一次形成等腰三角形；若不能，则说明理由；
一诺书业暑假作业快乐假期云南美术出版社系列答案科目：初中数学 来源： 题型：
【题目】某市质量技术监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
（1）若标准质量为450克，则抽样检测的20袋食品的总质量为多少克？
（2）若该种食品的合格标准为450±5g，求该食品的抽样检测的合格率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲乙两城市相距600千米，一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市．已知货车出发1小时后客车再出发，先到终点的车辆原地休息．在汽车行驶过程中，设两车之间的距离为s（千米），客车出发的时间为t（小时），它们之间的关系如图所示，则下列结论错误的是（ ）
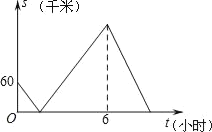
A. 货车的速度是60千米/小时
B. 离开出发地后，两车第一次相遇时，距离出发地150千米
C. 货车从出发地到终点共用时7小时
D. 客车到达终点时，两车相距180千米
查看答案和解析>>
科目：初中数学 来源： 题型：
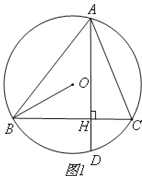
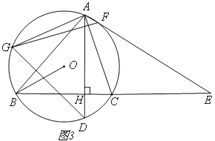
【题目】如图，△ABC内接于⊙O，弦AD⊥BC,垂足为H，连接OB.
(1)如图1,求证:∠DAC=∠ABO;
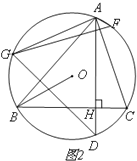
(2)如图2,在弧AC上取点F,使∠CAF=∠BAD,在弧AB取点G，使AG∥OB，若∠BAC=600，
求证:GF=GD;
(3)如图3,在(2)的条件下,AF、BC的延长线相交于点E,若AF：FE=1:9，求sin∠ADG的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
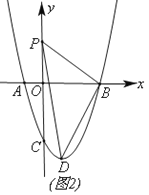
【题目】如图,在平面直角坐标中，抛物线y=ax2－2ax－3a(a≠0)与x轴交于A、B(A在B的左侧)，与y轴交于点C,且OC=3OA.
（1）如图（1）求抛物线的解析式；
（2）如图（2）动点P从点O出发，沿y轴正方向以每秒1个单位的速度移动，点D是抛物线顶点，连接PB、PD、BD，设点P运动时间为t（单位：秒），△PBD的面积为S，求S与t的函数关系式；
（3）如图（3）在（2）的条件下，延长BP交抛物线于点Q，过点O作OE⊥BQ，垂足为E，连接CE、CB，若CE=CB，求t值，并求出此时的Q点坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
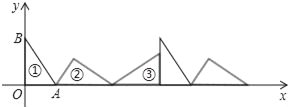
【题目】如图①为Rt△AOB，∠AOB=90°，其中OA=3，OB=4．将AOB沿x轴依次以A，B，O为旋转中心顺时针旋转．分别得图②，图③，…，则旋转到图⑩时直角顶点的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）化简求值: 2(x2y＋xy)－3(x2y－xy)－4x2y，其中x＝-1，y＝
.
（2）解答:老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
＋(－3x2＋5x－7)＝－2x2＋3x－6.求所捂的多项式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
线段
上，线段
，
，点
、
分别是线段
、
的中点.
（1）求线段
的长度；
（2）根据（1）中计算的结果，设
，其他条件不变，你能猜想线段的长度吗？
（3）若题中的条件变为“点在直线上”其它条件不变，则的长度会有变化吗？若有变化，请求出结果.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在以O为原点的直角坐标系中，抛物线的顶点为A （﹣1，﹣4），且经过点B（﹣2，﹣3），与x轴分别交于C、D两点．
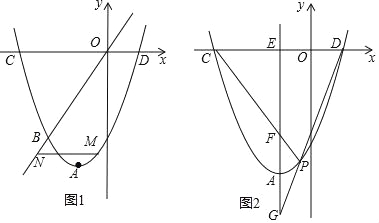
（1）求直线OB以及该抛物线相应的函数表达式；
（2）如图1，点M是抛物线上的一个动点，且在直线OB的下方，过点M作x轴的平行线与直线OB交于点N，求MN的最大值；
（3）如图2，过点A的直线交x轴于点E，且AE∥y轴，点P是抛物线上A、D之间的一个动点，直线PC、PD与AE分别交于F、G两点．当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
