
����Ŀ����ͼ����![]() Ϊֱ���İ�Բ����һ��
Ϊֱ���İ�Բ����һ��![]() ������
������![]() ����
����![]() ��
��![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ������Բ�ڵ�
������Բ�ڵ�![]() ����֪��
����֪��![]() ����
����![]() �ij���Ϊ
�ij���Ϊ![]() ��
��![]() �ij���Ϊ
�ij���Ϊ![]() ��
��![]() �ij���Ϊ
�ij���Ϊ![]() ������
������![]() ���
���![]() �غ�ʱ��
�غ�ʱ��![]() ��
��![]() ������
������![]() ���
���![]() �غ�ʱ��
�غ�ʱ��![]() ��
��![]() ����
����
С��ͬѧ����ѧϰ�����ľ��飬�ֱ�Ժ���![]() ��
��![]() ���Ա���
���Ա���![]() �仯���仯�Ĺ��ɽ�����̽����
�仯���仯�Ĺ��ɽ�����̽����
������С��ͬѧ��̽�����̣��벹��������
��1�������±����Ա���![]() ��ֵ����ȡ�㡢��ͼ���������ֱ�õ���
��ֵ����ȡ�㡢��ͼ���������ֱ�õ���![]() ��
��![]() ��
��![]() �ļ����Ӧֵ���벹ȫ����
�ļ����Ӧֵ���벹ȫ����
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| 5 | 2.85 | 1.98 | 1.52 | 1.21 | 0.97 | 0.76 | 0.56 | 0.37 | 0.19 | 0 |
| 0 | 0.46 | 1.29 | 1.61 | 1.84 | 1.96 | 1.95 | 1.79 | 1.41 | 0 |
��2����ͬһƽ��ֱ������ϵ![]() �У������ȫ��ı��и�����ֵ����Ӧ�ĵ�
�У������ȫ��ı��и�����ֵ����Ӧ�ĵ�![]() ��
��![]() ������������
������������![]() ��
��![]() ��ͼ��
��ͼ��
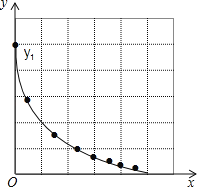
��3����Ϻ���ͼ������⣺
�ٵ�![]() ��
��![]() �ij�������
�ij�������![]() ʱ��
ʱ��![]() ���ȵ�ȡֵ��ΧԼ���� ��
���ȵ�ȡֵ��ΧԼ���� ��
�ڵ�![]() ��
��![]() ��
��![]() �ܷ�����
�ܷ�����![]() ΪԲ�ĵ�ͬһ��Բ�ϣ��� ��������������������
ΪԲ�ĵ�ͬһ��Բ�ϣ��� ��������������������
���𰸡���1��![]() ʱ��
ʱ��![]() ������������������2������ͼ����ͼ��ʾ������������3����
������������������2������ͼ����ͼ��ʾ������������3����![]() ���ڷ�
���ڷ�
��������
��1�����ò��������Խ�����⣻
��2��������㷨��������ͼ�ɣ�
��3��������ͼ���ɽ�����⣮������ͼ������⣬��Ϊ����![]() ��
��![]() �Լ�ֱ��
�Լ�ֱ��![]() �������ܽ���ͬһ�㣬���Բ���������
�������ܽ���ͬһ�㣬���Բ���������![]() �ĵ�
�ĵ�![]() �����Ե�
�����Ե�![]() ��
��![]() ��
��![]() ����������
����������![]() ΪԲ�ĵ�ͬһ��Բ��
ΪԲ�ĵ�ͬһ��Բ��
��1�����ò�������֪��![]() ʱ��
ʱ��![]() ����������������
����������������
��2������ͼ����ͼ��ʾ��
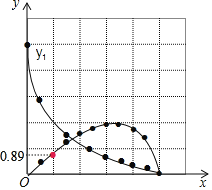
��3���ٹ۲�ͼ���֪����![]() ��
��![]() �ij�������
�ij�������![]() ʱ��
ʱ��![]() ���ȵ�ȡֵ��ΧԼ��
���ȵ�ȡֵ��ΧԼ��![]() ��
��
�ʴ�Ϊ![]() ��
��
��������![]() ��
��![]() �Լ�ֱ��
�Լ�ֱ��![]() �������ܽ���ͬһ�㣬
�������ܽ���ͬһ�㣬
���Բ���������![]() �ĵ�
�ĵ�![]() ��
��
���Ե�![]() ��
��![]() ��
��![]() ����������
����������![]() ΪԲ�ĵ�ͬһ��Բ��
ΪԲ�ĵ�ͬһ��Բ��
�ʴ�Ϊ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
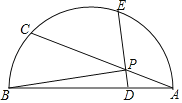
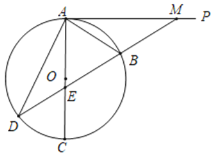
����Ŀ����ͼ��AC�ǡ�O��ֱ����AB�ǡ�O��һ���ң�AP�ǡ�O�����ߣ���BM��AB����AP���ڵ�M���ӳ�MB��AC�ڵ�E������O�ڵ�D������AD��
��1����֤��AB��BE��
��2������O�İ뾶R��2.5��MB��3����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]()
![]() ��
��![]() �������һ�����㣬���������������ۣ��ٸ������ߵĶԳ�����
�������һ�����㣬���������������ۣ��ٸ������ߵĶԳ�����![]() ���Ҳࣻ�ڹ���
���Ҳࣻ�ڹ���![]() �ķ���
�ķ���![]() ��ʵ��������
��ʵ��������![]() �����У���ȷ���۵ĸ���Ϊ�� ��
�����У���ȷ���۵ĸ���Ϊ�� ��
A.0��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
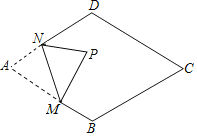
����Ŀ����ͼ��������ABCD�У���A��60����AB��6����MΪAB����һ�㣬AM��4����NΪAD���ϵ�һ���㣬��MN����AMN���ۣ���A���ڵ�P��������P�����εĶԽ�����ʱ��AN�ij���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
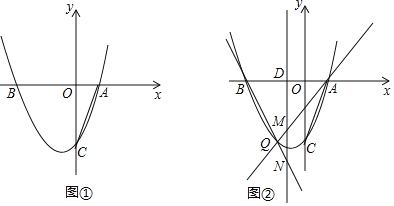
����Ŀ����ͼ��������y��x2+bx+c��x����A��B���㣬���е�A����Ϊ��1��0������y�ύ�ڵ�C��0����3����
��1���������ߵĺ�������ʽ��
��2����ͼ�٣�����AC����P���������ϣ��������PAB��2��ACO�����P�����ꣻ
��3����ͼ�ڣ���QΪx���·�������������һ�㣬��D�������߶Գ�����x��Ľ��㣬ֱ��AQ��BQ�ֱ������ߵĶԳ����ڵ�M��N������DM+DN�Ƿ�Ϊ��ֵ������ǣ�����������ֵ��������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
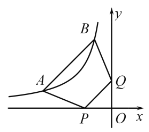
����Ŀ����ͼ����A��a��1����B��b��3������˫����![]() �ϣ���P��Q�ֱ���x�ᣬy���ϵĶ��㣬���ı���ABQP�ܳ�����СֵΪ�� ��
�ϣ���P��Q�ֱ���x�ᣬy���ϵĶ��㣬���ı���ABQP�ܳ�����СֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ϣ�С����С��Ҫ����С�Ӷ�����BC�ĸ߶ȣ�С���ڵ�A��ô�������B������Ϊ45�㣬С����A�������б����![]() ����б���ϵ�D���ڴ˴���������˵�B������Ϊ31�㣬��б��AF���±�Ϊ1��2��
����б���ϵ�D���ڴ˴���������˵�B������Ϊ31�㣬��б��AF���±�Ϊ1��2��
��1����С���ӵ�A����D�Ĺ����У��������ĸ߶ȣ�
��2���������Dz����������ܷ��������BC�ĸ߶ȣ����ܣ�����㣻�����ܣ���˵�����ɣ����ο����ݣ�sin31���0.52��cos31���0.86��tan31���0.60��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����������x���ཻ��M��N����(��M�ڵ�N�����)���䶥��P���߶�AB���ƶ�����A��B������ֱ�Ϊ(-2��-3)��(1��-3)����N�ĺ���������ֵΪ4�����M�ĺ��������СֵΪ( )

A.-1 B.-3C.-5D.-7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
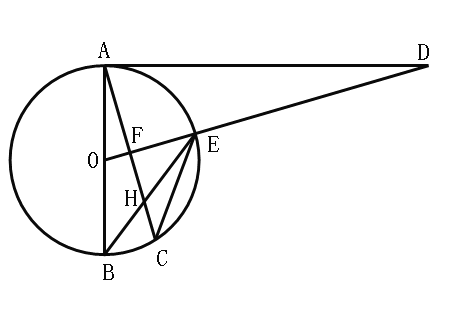
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬![]() �ڵ�F������O�ڵ�E��AC��BE�ڵ�H����DΪOE�ӳ����ϵ�һ�㣬�ҡ�ODA=��BEC��
�ڵ�F������O�ڵ�E��AC��BE�ڵ�H����DΪOE�ӳ����ϵ�һ�㣬�ҡ�ODA=��BEC��
��1����֤��AD�ǡ�O�����ߣ�
��2����֤��![]() ��
��
��3������O�İ뾶Ϊ5��![]() ����AH�ij���
����AH�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com