
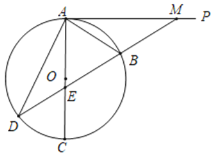
【题目】如图,AC是⊙O的直径,AB是⊙O的一条弦,AP是⊙O的切线,作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=2.5,MB=3,求AD的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据切线的性质得出∠MAE=90°,由等角的余角相等得出∠BAE=∠AEB,进而得证;
(2)根据圆周角定理的推论得出∠ABC=90°,进而可证明△ABC∽△EAM,利用相似三角形的性质求出AM,由圆周角定理证明∠AMB=∠D即可.
(1)证明:∵AC为直径,AP是⊙O的切线,
∴∠MAE=90°,
∴∠MAB+∠BAE=90°,∠AMB+∠AEB=90°,
∵BM=BA,
∴∠BAM=∠BMA,
∴∠BAE=∠AEB,
∴AB=BE;
(2)解:连接BC,∵AC为直径,
∴∠ABC=90°,
∵∠BAE=∠BEA,∠MAE=∠ABC=90°,
∴△ABC∽△EAM,
∴![]() ,∠AMB=∠C,
,∠AMB=∠C,
即![]() ,
,
解得,![]() ,
,
又∵∠C=∠D,
∴∠AMB=∠D
∴![]() .
.


科目:初中数学 来源: 题型:
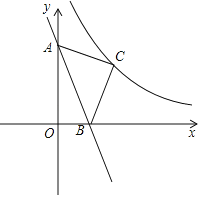
【题目】如图,在平面直角坐标系中,将直线y=﹣3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=![]() (x>0)的图象经过点C,求此反比例函数的表达式.
(x>0)的图象经过点C,求此反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植![]() 、
、![]() 两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了
两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了![]() 种核桃
种核桃![]() 亩.
亩.
(Ⅰ)若该基地收获两种核桃的年总产量为25 800千克,则![]() 、
、![]() 两种核桃各种植了多少亩?
两种核桃各种植了多少亩?
(Ⅱ)全部收购后,总收入为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式.若要求种植
之间的函数关系式.若要求种植![]() 种核桃的面积不少于
种核桃的面积不少于![]() 种核桃的一半,那么种植
种核桃的一半,那么种植![]() 种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
解:(Ⅰ)先用含![]() 的代数式填空,再完成解答.
的代数式填空,再完成解答.
由种植了![]() 种核桃
种核桃![]() 亩,可知
亩,可知![]() 种核桃种植的亩数为________,则
种核桃种植的亩数为________,则![]() 种核桃的年总产量为________千克,
种核桃的年总产量为________千克,![]() 种核桃的年总产量为________千克.
种核桃的年总产量为________千克.
根据题意列出方程________________________;
解得:
(Ⅱ)
查看答案和解析>>
科目:初中数学 来源: 题型:
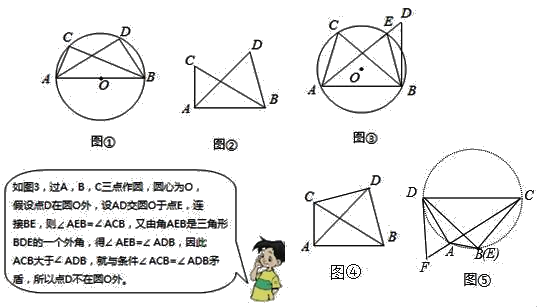
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=4,点D的坐标是(6,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为__________.
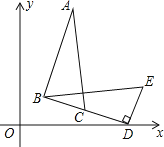
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行趣味运动会共有三个项目:A.“协力竞走”、B.“快乐接力”、C.“摸石过河”.小明和小刚参与了该运动会的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到A.“协力竞走”项目组的概率为 ;
(2)列表或画树状图求小明和小刚被分配到同一项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月10日,光明中学团委利用网络平台组织八年级600名学生参加“全民抗疫”知识大赛.为了了解本次大赛的成绩,随机抽取了部分学生的成绩作为样本,按![]() ,
,![]() ,
,![]() ,
,![]() 四个等级进行统计,制成如下不完整的统计图.
四个等级进行统计,制成如下不完整的统计图.
(说明:![]() 级80分-100分,
级80分-100分,![]() 级70分-79分,
级70分-79分,![]() 级60-69分,
级60-69分,![]() 级0分-59分)
级0分-59分)
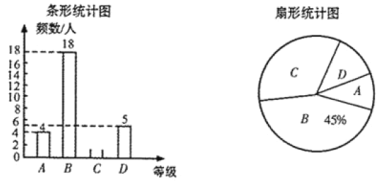
根据所给信息,解答以下问题:
(1)在扇形统计图中,![]() 级对应的扇形的圆心角是______度;
级对应的扇形的圆心角是______度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在______等级;
(4)若成绩达到![]() 等级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?
等级的学生可以选为志愿者,请估计该校八年级600名学生中可以选为志愿者学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以![]() 为直径的半圆上有一点
为直径的半圆上有一点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一个动点,连接
上一个动点,连接![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交半圆于点
,交半圆于点![]() .已知:
.已知:![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ).
).
小青同学根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 变化而变化的规律进行了探究.
变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值,请补全表格;
的几组对应值,请补全表格;
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| 5 | 2.85 | 1.98 | 1.52 | 1.21 | 0.97 | 0.76 | 0.56 | 0.37 | 0.19 | 0 |
| 0 | 0.46 | 1.29 | 1.61 | 1.84 | 1.96 | 1.95 | 1.79 | 1.41 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
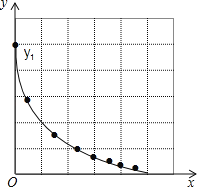
(3)结合函数图象,解决问题:
①当![]() ,
,![]() 的长都大于
的长都大于![]() 时,
时,![]() 长度的取值范围约是 ;
长度的取值范围约是 ;
②点![]() ,
,![]() ,
,![]() 能否在以
能否在以![]() 为圆心的同一个圆上? (填“能”或“否”)
为圆心的同一个圆上? (填“能”或“否”)
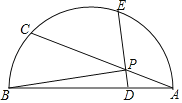
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com