
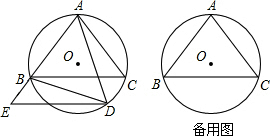
 如图,⊙O是△ABC的外接圆,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD,且∠ADB=∠E.
如图,⊙O是△ABC的外接圆,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD,且∠ADB=∠E.分析 (1)欲证明AB=AC,可以通过∠C=∠ABC来推知.利用圆周角定理和平行线的性质进行证明即可;
(2)根据切线的定义知:当AD⊥ED时,DE是⊙O的切线;
(3)如备用图,连接AO并延长交BC于F,连接OB,OC.构建直角△ABF、△OBF.在这两个直角三角形中利用勾股定理来求⊙O的半径.
解答 解:(1)证明:∵∠ADB与∠C都是$\widehat{AB}$所对的圆周角,
∴∠ADB=∠C.
又∵∠ADB=∠E,
∴∠C=∠E.
又∵DE∥BC,
∴∠E=∠ABC,
∴∠C=∠ABC,
∴AB=AC;
(2)当D运动到$\widehat{BC}$的中点时,DE是⊙O的切线,理由如下:
∵$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD,AB=AC,
∴AD是BC的垂直平分线,
∴AD是直径且AD⊥BC,
∴AD过圆心O.
又∵DE∥BC,
∴AD⊥ED,
∴DE是⊙O的切线;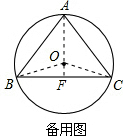
(3)如备用图,连接AO并延长交BC于F,连接OB,OC.
∵AB=AC,OB=OC,
∴AO垂直平分BC,
∴BF=CF=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3.
在直角△ABF中,由勾股定理可得 AF=4.
设⊙O的半径为r,在直角△OBF中,OB=r,BF=3,OF=4-r,
∴r2=32+(4-r)2,
解得 r=$\frac{25}{8}$,
∴⊙O的半径是$\frac{25}{8}$.
点评 本题考查了切线的判定和勾股定理.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,面积为96cm2的长方形,长是宽的2倍,四个角是面积为3cm2的小正方形,现将四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(精确到0.1cm,参考数据:$\sqrt{3}$=1.732)
如图,面积为96cm2的长方形,长是宽的2倍,四个角是面积为3cm2的小正方形,现将四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(精确到0.1cm,参考数据:$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{18}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{4}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
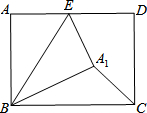 如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠BCD的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰落在∠BCD的平分线上时,CA1的长为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}±1$ | C. | 2$\sqrt{2}$±1 | D. | $\sqrt{6}±\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
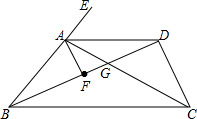 如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )
如图,BD平分∠ABC,AF平分∠BAD,∠EAD=2∠DBC,∠BDC=∠AFB,下列结论:①AD∥BC;②∠AFB=90°;③∠FAG=∠DCG,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ① | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
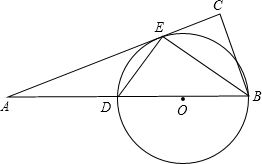 如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE
如图,BD是⊙O的直径,E是⊙O上的一点,直线AE交BD的延长线于点A,BC⊥AE于C,且∠CBE=∠DBE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com