
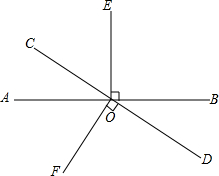
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,如果∠AOC=$\frac{1}{5}$∠EOF(∠EOF指图中钝角),求∠AOC的度数.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,如果∠AOC=$\frac{1}{5}$∠EOF(∠EOF指图中钝角),求∠AOC的度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
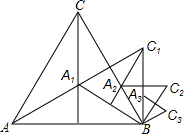 如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.
如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
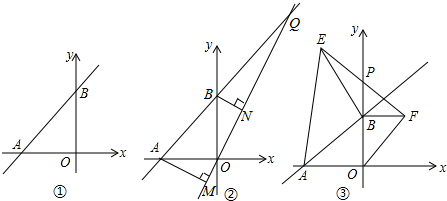
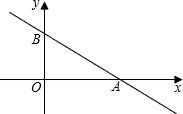 如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.
如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=$-\frac{3}{4}x+3$与直线y=$kx-\frac{16}{3}$交于x轴上的同一个点A,直线y=$-\frac{3}{4}x+3$与y轴交于点B,直线y=$kx-\frac{16}{3}$与y轴的交点为C.
已知直线y=$-\frac{3}{4}x+3$与直线y=$kx-\frac{16}{3}$交于x轴上的同一个点A,直线y=$-\frac{3}{4}x+3$与y轴交于点B,直线y=$kx-\frac{16}{3}$与y轴的交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
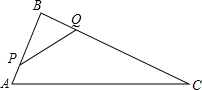 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com