练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图所示，在△ABC中，∠A=90°，BD平分∠ABC，AD=2cm，AB+BC=8，S△ABC=8cm2．

    分析 过点D作DE⊥BC于E，根据角平分线上的点到角的两边距离相等可得AD=DE，再根据S△ABC=S△ABD+S△BCD列式计算即可得解．

    解答 解：如图，过点D作DE⊥BC于E，
    ∵∠A=90°，BD平分∠ABC，
    ∴AD=DE=2cm，
    ∵AB+BC=8，
    ∴S△ABC=S△ABD+S△BCD
    =$\frac{1}{2}$×8×2
    =8cm2．
    故答案是：8cm2．

    点评 本题考查了角平分线上的点到角的两边距离相等的性质，三角形的面积，熟记性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

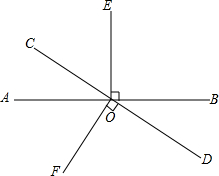    3．如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD，如果∠AOC=$\frac{1}{5}$∠EOF（∠EOF指图中钝角），求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

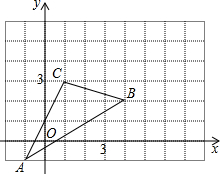    4．如图，△ABC在直角坐标系中，
    （1）请写出△ABC各点的坐标．
    （2）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化位置，并写出A′、B′、C′的坐标．
    （3）求出S△ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知扇形的弧长为2πcm，圆心角为120°，则扇形的面积为3πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

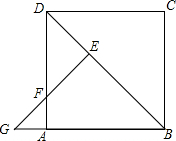    8．如图，连接正方形ABCD的对角线BD，把△BCD绕点B按逆时针方向旋转45°得到△BEG，此时EG交AD于点F．如果AD=1，那么AF=$\sqrt{2}-1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知点A（-1，y1）、B（0.5，y2）在反比例函数$y=\frac{5}{x}$图象上，则有（　　）
    A．y1＜0＜y2B．y2＜0＜y1C．y1＜y2＜0D．y2＜y1＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在平行四边形ABCD中，点E、F分别在AD、BC上，且AE=CF．求证：BE∥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知M（1，2），则M关于原点的对称点N落在（　　）
    A．y=$\frac{1}{x}$的图象上B．y=-$\frac{1}{x}$的图象上C．y=$\frac{2}{x}$的图象上D．y=-$\frac{2}{x}$的图象上

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

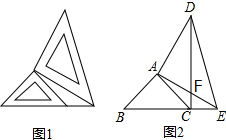    3．两块不相等的等腰直角三角形如图1放置，图2是它们抽象出的几何图形，点B、C、E在同一条直线上，连接CD，AE、CD交于点F，请你在不添加线段或字母的情况下：
    （1）找出一对全等三角形并证明；
    （2）找出一对相似但不全等的三角形，并证明（△ABC∽△AED除外）．

    查看答案和解析>>

    同步练习册答案