
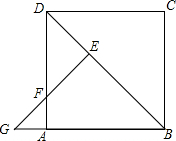
 如图,连接正方形ABCD的对角线BD,把△BCD绕点B按逆时针方向旋转45°得到△BEG,此时EG交AD于点F.如果AD=1,那么AF=$\sqrt{2}-1$.
如图,连接正方形ABCD的对角线BD,把△BCD绕点B按逆时针方向旋转45°得到△BEG,此时EG交AD于点F.如果AD=1,那么AF=$\sqrt{2}-1$. 分析 如图,首先运用正方形的性质、旋转变换的性质证明BE=BC=1,BG=BD=$\sqrt{2}$;其次证明DF=GF,此为解决该题的关键性结论;运用勾股定理列出关于DF的方程,求出DF即可解决问题.
解答  解:如图,∵四边形ABCD为正方形,且边长为1,
解:如图,∵四边形ABCD为正方形,且边长为1,
∴∠C=90°,CD=CB=1,
∴$BD=\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2}$;由题意得:
BE=BC=1,BG=BD=$\sqrt{2}$,
∴DE=AG=$\sqrt{2}$-1;而∠DEF=∠GAF=90°,∠DFE=∠GFA,
∴△DEF∽△GAF,
∴$\frac{DE}{AG}=\frac{DF}{GF}$=1,
∴DF=GF(设为λ),则AF=1-λ,
由勾股定理得:${λ}^{2}=(\sqrt{2}-1)^{2}+(1-λ)^{2}$,
解得:λ=2-$\sqrt{2}$,
∴AF=1-λ=$\sqrt{2}-1$,
故答案为$\sqrt{2}$-1.
点评 该题主要考查了旋转变换的性质、正方形的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;解题的关键是牢固掌握旋转变换的性质、正方形的性质等知识点,并能灵活运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
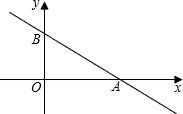 如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.
如图,直线y=kx+3与x轴、y轴分别交于A、B两点,$\frac{OB}{OA}$=$\frac{3}{4}$,点C是直线y=kx+3上与A、B不重合的动点,过点C的另一直线CD与y轴相交于点D,是否存在点C使△BCD与△AOB全等?若存在,求出点C的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com