
����Ŀ����֪����ͼ��ʾ���ھ���ABCD�У���E��BC���ϣ���AEF��90��
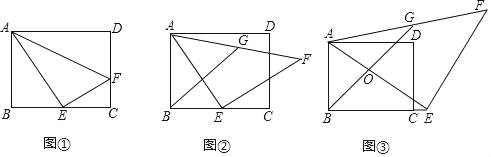
��1����ͼ�٣���֪��F��CD���ϣ�AD��AE��5��AB��4����DF�ij���
��2����ͼ�ڣ���֪AE��EF��GΪAF���е㣬��̽���߶�AB��BE��BG��������ϵ��
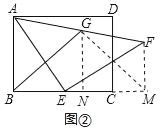
��3����ͼ�ۣ���E�ھ���ABCD��BC�ߵ��ӳ����ϣ�AE��BG�ཻ��O�㣬���������루2�����ֲ��䣬AD��5��AB��4��CE��1�����AOG�������
���𰸡���1��![]() ����2��AB+BE��
����2��AB+BE��![]() BG�����ɼ���������3��
BG�����ɼ���������3��![]()
��������
��1�����ݾ����������AE,���ù��ɶ�����BE,EC,��֤Rt��AEF��Rt��ADF��HL������Rt��CEF�У��ɹ��ɶ����ý������2����FM��BC��BC���ӳ�����M����GN��BC��N������GM����ABE�ա�EMF��AAS������AB��EM��BE��FM��֤��NΪBM���е㣬GN��![]() ��AB+FM�����ٽ�ֱ�������οɵã���3������EG����OP��BE��P����OQ��AG��Q�����ݾ������ʣ�֤������ֱ�������Σ��ٽ�ֱ�������Σ�����ؼ��߶γ��ȣ��������.
��AB+FM�����ٽ�ֱ�������οɵã���3������EG����OP��BE��P����OQ��AG��Q�����ݾ������ʣ�֤������ֱ�������Σ��ٽ�ֱ�������Σ�����ؼ��߶γ��ȣ��������.
��1�����ı���ABCD�Ǿ��Σ�
���A����C����D��90����CD��AB��4��
��AD��AE��AD��5��
��AE��5��
��Rt��ABE�У��ɹ��ɶ����ã�BE��![]() ��3��
��3��
��EC��2��
��Rt��AEF��Rt��ADF��![]() ��
��
��Rt��AEF��Rt��ADF��HL����
��EF��DF��
��DF��EF��x����CF��4��x��
��Rt��CEF�У��ɹ��ɶ����ã�22+��4��x��2��x2��
��ã�x��![]() ��
��
��DF�ij�Ϊ![]() ��
��
��2��AB+BE��![]() BG���������£�
BG���������£�
��FM��BC��BC���ӳ�����M����GN��BC��N������GM����ͼ����ʾ��
�ڡ�ABE�͡�EMF�У�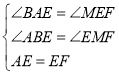 ��
��
���ABE�ա�EMF��AAS��
��AB��EM��BE��FM��
��AB��BC��FM��BC��GN��BC��
��AB��GN��FM���ֵ�GΪAF���е㣬
���NΪBM���е㣬GN��![]() ��AB+FM����
��AB+FM����
��GN��![]() BM��
BM��
��GB��GN����BGM��90����
��BM��![]() BG��
BG��
��AB+BE��![]() BG��
BG��
��3������EG����OP��BE��P����OQ��AG��Q����ͼ����ʾ��
���ı���ABCD�Ǿ��Σ�
��BC��AD��5����ABC��90����
��BE��BC+CE��6��
��AE��![]()
�ߡ�AEF�ǵ���ֱ�������Σ�G��AF���е㣬
���GAE��45����EG��AF��
���AGE�ǵ���ֱ�������Σ���AGE��90����
��AE��![]() AG��
AG��
��AG��![]() ��
��
�ߡ�ABE��90����
���ABE+��AGE��180����
��A��B��E��G�ĵ㹲Բ��
���GBE����GAE��45����
���OBP�ǵ���ֱ�������Σ�
��OP��BP��
��OP��BP��x��
��tan��AEB��![]() ��
��
��![]() ��
��
��PE��![]() x��
x��
��BP+PE��BE��6��
��x+![]() x��6��
x��6��
��ã�x��![]() ��
��
��OP��![]() ��
��
��OE��![]() ��
��
��AO��AE��OE��![]() ��
��
��Rt��AOQ����OAQ��45����
��OQ��![]() ��
��
���AOG�������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
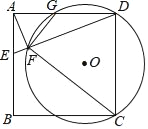
����Ŀ����ͼ����������ABCD�У�E��AB��һ�㣬����DE������A��AF��DE������ΪF����O������C��D��F����AD�ཻ�ڵ�G��
��1����֤����AFG�ס�DFC��
��2����������ABCD�ı߳�Ϊ4��AE��1������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ְ�����С��һ�������һ�����г���Ϊ��������ڼס������̳�������ͬ������г�������ͬ���������Ҳ��ͬ�����г����������֮��Ϊ452Ԫ�������г��ĵ��۱�����ĵ���4����8Ԫ��
��1�������г���������۸�Ϊ����Ԫ��
��2���������ٸ����̼Ҵ��������̳�������Ʒ������ۣ���8.5�ۣ����ۣ���ȫ�������100Ԫ������ȯ30Ԫ��������100Ԫ����ȯ����100Ԫ��30Ԫ����ȯ����200Ԫ��60Ԫ����ȯ�������ɵ������ڹ������ȯȫ��ͨ�ã����ְ�ֻ����400ԪǮ�������ֻ��ͬһ���̳������е�������Ʒ������һ�����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�߿Ƽ���˾����һ�־������Ͳ��ϰ壬�䳤��֮��Ϊ 3��2��ÿ�Ų��ϰ�ijɱ� c�������������������ÿ�Ų��ϰ�����ۼ۸� y����� x ֮����������ѧϰ����ij�ֺ�����ϵ(��һ�κ����������������Ͷ��κ�����ϵ�е�һ��)���±���¼�˸ù������������۸ò��ϰ�һЩ���ݣ�
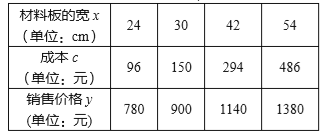
��1����һ�Ų��ϰ�����۸� y ��� x ֮��ĺ�����ϵʽ ������д���Ա��ȡֵ��Χ��
��2����һ�Ų��ϰ������ w Ϊ���ۼ۸� y��ɱ� c �IJ�
����ֱ��д��һ�Ų��ϰ������ w ��� x ֮��ĺ�����ϵ ������д���Ա��ȡֵ��Χ��
�ڵ����ϰ�Ŀ�Ϊ����ʱ��һ�Ų��ϰ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1���������½��ۣ���abc��0 ��b2��4ac��0 ��4b+c��0 ����B����![]() ��y1����C����
��y1����C����![]() ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2������3��x��1ʱ��y��0��
������ȷ�Ľ����ǣ���д������ȷ���۵���ţ�__________________��
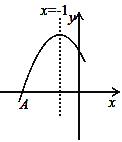
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�˸����280��ѧ������Ů������������ͬ������С��Ϊ����ѧ�������ʽ���ˮƽ����չ��һ�ε����о����뽫����Ĺ��̲�ȫ.
�ռ����ݣ�
(1)����С��ƻ�ѡȡ40��ѧ�������ʽ������Գɼ���Ϊ�����������ȡ�������У���������___________������ĸ����
A����ȡ���꼶1�ࡢ2���20��ѧ�������ʽ������Գɼ��������
B����ȡ���������ɼ��Ϻõ�ѧ����40��ѧ�������ʽ������Գɼ��������
C�����꼶�а�ѧ�����ѡȡ��Ů����20��ѧ��ѧ�������ʽ������Գɼ��������
�������������ݣ�
��������ȷ������С������40��ѧ�������ʽ������Գɼ����£�
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
�������ݣ����±���ʾ��
2018����꼶����ѧ��ѧ�������ʽ������Գɼ�ͳ�Ʊ�
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
�������ݡ��ó�����
����С�齫ͳ�ƺ��������ȥ��ͬ�ھ��꼶��ѧ�������ʽ������Գɼ���ֱ��ͼ�������˶Աȣ�
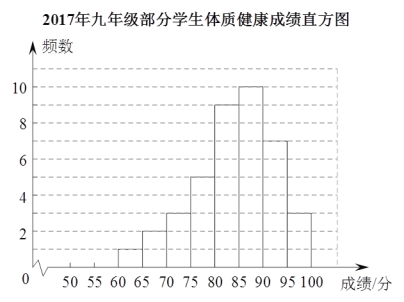
(2)���ܴ��еõ��Ľ�����_____________�����������________________________________.
(3)������ʦ�ƻ�����2018���ͳ�����ݰ���75�����µ�ͬѧ�μ����ʼ�ǿѵ����Ŀ����ȫ�꼶Լ��________��ͬѧ�μӴ���Ŀ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��4��22���ǵ�50����������գ�ijУ�ڰ��꼶5�����У�ÿ���ѡ��10��ѧ���μ�������֪ʶ��������������һ���������Ƚ�����������ѧУ������������ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ���������ͼ����Ϣ����������⣺
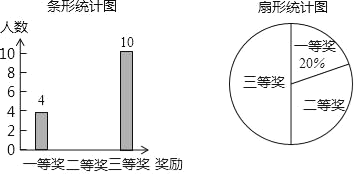
��1���ξ�����������������ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�������Ƚ�������Ӧ���ε�Բ�ĽǶ�����
��3�������У���꼶��800�ˣ�������ƻ�ͬѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������aʹ����x�IJ���ʽ�� ������3�������⣬��ʹ����y�ķ�ʽ����
������3�������⣬��ʹ����y�ķ�ʽ����![]() ��2�зǸ������⣬��������������������a�ĺ���(����)
��2�зǸ������⣬��������������������a�ĺ���(����)
A. 14B. 15C. 23D. 24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y��mx+n�Ͷ��κ���y��mx2+nx+1������m��0��
��1�������κ���y��mx2+nx+1�����㣨2��0������3��1�����Էֱ�������������Ľ���ʽ��
��2����һ�κ���y��mx+n�����㣨2��0������ͼ����һ�������ޣ����κ���y��mx2+nx+1�����㣨a��y1���ͣ�a+1��y2������y1��y2�������a��ȡֵ��Χ��
��3�������κ���y��mx2+nx+1�Ķ�������ΪA��h��k����h��0����ͬʱ���κ���y��x2+x+1Ҳ����A�㣬��֪��1��h��1�������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com