
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ。以下五个结论:
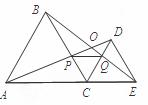
① AD=BE;② PQ∥AE;③ AP=BQ;④ DE=DP; ⑤ ∠AOB=60°成立的结论个数是( )
A.2 B.3 C.4 D.5
C
【解析】由于△ABC和△CDE是等边三角形,所以AC=BC,CD=CE,∠ACB=∠DCE=60°,所以△ACD≌△BCE,从而AD=BE,故①正确;由△ACD≌△BCE得∠CBE=∠DAC,又因为∠ACB=∠DCE=60°,AC=BC,所以△ACP≌△BCQ,所以AP=BQ;故③正确;因为△CQB≌△CPA,再根据∠PCQ=60°得到△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,故②正确;根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,所以∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,故⑤正确.共4个正确结论。
故选C.


科目:初中数学 来源: 题型:
如图(1),抛物线 (
( )与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为
)与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为 ,抛物线的对称轴与
,抛物线的对称轴与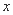 轴交于点E,点D(-2,-3)在对称轴上.
轴交于点E,点D(-2,-3)在对称轴上.

(1)求此抛物线的解析式;
(2)如图(1),若点M是线段OE 上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;
上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;
(3)如图(2),过点B作BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿GH边翻折得△DGH,求当KG为何值时,△DGH与△KGH重叠部分的面积是△DGK面积的 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )


查看答案和解析>>
科目:初中数学 来源: 题型:
请选择一组你自己所喜欢的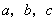 的值,使二次函数
的值,使二次函数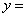
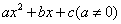 的图象同时足下列条件:①开口向下,②当x<-2时,
的图象同时足下列条件:①开口向下,②当x<-2时,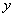 随
随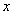 的增大而增大;当x>-2时,
的增大而增大;当x>-2时,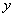 随
随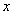 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com