
【题目】如图,反比例函数y=![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为9,则k的值为( )
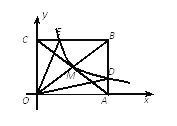
A. 3B. 6C. 9D. 4
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=![]() AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求![]() 的值,并直接写出
的值,并直接写出![]() 的值.
的值.
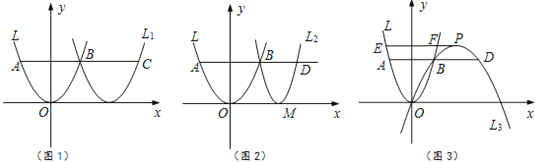
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD 中,AB=4,AD=a,点P在AD上,且AP=2,点E是边AB上的动点,以PE为边作直角∠EPF,射线PF交BC于点F,连接EF,给出下列结论:①tan∠PFE=![]() ;②a的最小值为10.则下列说法正确的是( )
;②a的最小值为10.则下列说法正确的是( )
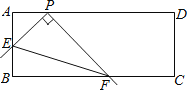
A.①②都对B.①②都错C.①对②错D.①错②对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,点D是BC上任意点,以AD为边作∠ADE=∠ADF=60°,分别交AC,AB于点E,F.
(1)求证:AD2=AE×AC
(2)已知BC=2,设BD的长为x,AF的长为y,求y关于x的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=8,AD=6;点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H.

(1)如图2,当点F与点B重合时,求CE和CG的长;
(2)如图3,当点E是BD中点时,求CE和CG的长;
(3)在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
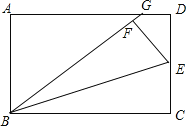
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线![]() 与x轴的两个交点为A,B(点A在点B的左侧,顶点为P,连接PA,PB,那么称
与x轴的两个交点为A,B(点A在点B的左侧,顶点为P,连接PA,PB,那么称![]() PAB为这条抛物线的“抛物线三角形”。
PAB为这条抛物线的“抛物线三角形”。
(1)请写出“抛物线三角形”是等腰直角三角形时,抛物线的表达式(写出一个即可);
(2)若抛物线![]() 的“抛物线三角形”是等边三角形,求b的值;
的“抛物线三角形”是等边三角形,求b的值;
(3)若抛物线![]() 不存在“抛物线三角形”则a,b,c之间应满足怎样的关系式?请直接写出关系式。
不存在“抛物线三角形”则a,b,c之间应满足怎样的关系式?请直接写出关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com